观察下列等式据此规律.第n个等式可为1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$+-+$\frac{1}{2n-1}$-$\frac{1}{2n}$=$\frac{1}{n+1}$+$\frac{1}{n+2}$+-+$\frac{1}{2n}$．题目和参考答案——青夏教育精英家教网—

10．观察下列等式

据此规律，第n个等式可为1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n}$=$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$．

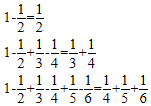
分析根据等式，左边有2n项，右边第一项分母为n+1，最后一项分母为n+n=2n，即可得出结论．

解答解：根据等式，左边有2n项，右边第一项分母为n+1，最后一项分母为n+n=2n．
据此规律，第n个等式可为1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n}$=$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$．
故答案为：1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n}$=$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$．

点评本题是规律探究题，考查观察与归纳推理的能力，比较基础．

练习册系列答案

68所名校图书小学毕业升学考前突破系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

5．已知θ为第二象限角，若tan（θ+$\frac{π}{4}$）=$\frac{1}{2}$，则sinθ-cosθ的值为（　　）

A．

$-\frac{{\sqrt{10}}}{5}$

B．

$\frac{{\sqrt{10}}}{5}$

C．

$\frac{{2\sqrt{10}}}{5}$

D．

$-\frac{{2\sqrt{10}}}{5}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

1．已知函数f（x）=ax²+ln（x+1）
（1）当a=-$\frac{1}{4}$时，求函数f（x）的单调区间
（2）当x∈[0，+∞）时，函数y=f（x）图象上的点都在$\left\{\begin{array}{l}{x≥0}\\{y-x≤0}\end{array}\right.$所表示的平面区域内，求实数a的取值范围
（3）求证：（1+$\frac{2}{2×3}$）（1+$\frac{4}{3×5}$）（1+$\frac{8}{5×9}$）…[1+$\frac{{2}^{n}}{（{2}^{n-1}+1）（{2}^{n}+1）}$]＜e（其中n∈N⁺，e是自然数的底数）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

18．随着智能手机的发展，微信越来越成为人们交流的一种方式，某机构对使用微信交流的态度进行调查，随机调查了50人，他们年龄的频数分布及对使用微信交流赞成人数如下表：

年龄（岁）	[15，25）	[25，35）	[35，45）	[45，55）	[55，65）	[65，75）
频数	5	10	15	10	5	5
赞成人数	5	10	12	7	2	1

（Ⅰ）由以上统计数据填写下面2×2列联表，关判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异；

	年龄不低于45岁的人数	年龄低于45岁的人数	合计
赞成	10	27	37
不赞成	10	3	13
合计	20	30	50

（Ⅱ）若对年龄在[55，65）的被调查人中随机抽取两人进行追踪调查，求至少有1人赞成使用微信交流的概率．
参考公式：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
参考数据：

P（K²≥k₀）	0.050	0.010	0.001
k₀	3.841	6.635	10.828

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．在直角坐标系xOy中，曲线${C_1}：\left\{{\begin{array}{l}{x=1+cosθ}\\{y=sinθ}\end{array}}\right.$（θ为参数），点P是曲线C₁与x轴正半轴的交点．在以O为极点，x轴正半轴为极轴的极坐标系轴，曲线C₂：ρcosθ+ρsinθ+3=0．
（1）求曲线C₁的极坐标方程和过点P的曲线C₁的切线极坐标方程；
（2）在曲线C₁上求一点Q（a，b），它到曲线C₂的距离最长．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

15．已知函数f（x）=$\sqrt{3}$sinωxcosωx-cos²ωx+$\frac{3}{2}$（ω∈R）的最小正周期为π，且图象关于直线x=$\frac{π}{6}$对称．
（1）求f（x）的解析式；
（2）求f（x）的单调递增区间；
（3）若函数g（x）=f（-x）+a（0$≤x≤\frac{π}{2}$）有且只有一个零点，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

2．