
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据题意,依次分析所给的4个命题:对于①、结合函数的奇偶性与单调性的性质,分析可得f(x)在区间[0,1]上为减函数,又由θ∈($\frac{π}{4}$,$\frac{π}{2}$),有sinθ>cosθ,则有f(sinθ)<f(cosθ);故①错误;对于②、利用诱导公式分析可得sin($\frac{π}{2}$-α)>sinβ,又由正弦函数的性质,则有$\frac{π}{2}$-α>β,即α+β<$\frac{π}{2}$;故②正确;对于③、将f(x)的解析式变形可得f(x)=-2sin(2x-$\frac{π}{3}$)+1,令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,解可得f(x)的递增区间,可得③错误;对于④、结合余弦函数的性质分析可得④错误;综合可得答案.
解答 解:根据题意,依次分析所给的4个命题:
对于①、f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,则f(x)在区间[0,1]上为减函数,
又由θ∈($\frac{π}{4}$,$\frac{π}{2}$),有sinθ>cosθ,则有f(sinθ)<f(cosθ);故①错误;
对于②、若锐角α、β满足cosα>sinβ,即sin($\frac{π}{2}$-α)>sinβ,又由0<$\frac{π}{2}$-α<$\frac{π}{2}$、0<β<$\frac{π}{2}$,
则有$\frac{π}{2}$-α>β,即α+β<$\frac{π}{2}$;故②正确;
对于③、f(x)=2sin($\frac{π}{3}$-2x)+1=-2sin(2x-$\frac{π}{3}$)+1,令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,
解可得kπ+$\frac{5π}{12}$≤x≤kπ+$\frac{11π}{12}$,
其单调递增区间为[kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],故③错误;
对于④、若cos(x+$\frac{π}{6}$)≥-$\frac{\sqrt{3}}{2}$,则有2kπ-$\frac{5π}{6}$≤x+$\frac{π}{6}$≤2kπ+$\frac{5π}{6}$,解可得2kπ-π≤x+$\frac{π}{6}$≤2kπ+$\frac{2π}{3}$,
即cos(x+$\frac{π}{6}$)≥-$\frac{\sqrt{3}}{2}$的解集为{x|2kπ-π≤x≤2kπ+$\frac{2π}{3}$,k∈Z};故④错误;
四个命题中,只有②是正确的;
故选:B.
点评 本题考查命题真假的判断,涉及知识点较多,注意要熟悉常见的知识点的应用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$+$\frac{1}{3}$i | B. | $\frac{2}{3}$-$\frac{1}{3}$i | C. | $\frac{6}{5}$+$\frac{3}{5}$i | D. | $\frac{6}{5}$-$\frac{3}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$,-1 | B. | $\frac{1}{2}$,1 | C. | $\frac{1}{2}$,-1 | D. | -$\frac{1}{2}$,1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
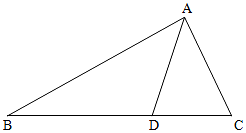 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com