
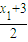 ,
,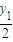 ).设D、E是圆C上的两个点,且DE垂直于x轴,DE的中点为H,点D(x2,y2),则H(x2,y3),求得|DC|和|CH|、|DH|2,可得当x2=2时,|DH|2=2,故弦长为|DE|=2|DH|=2
).设D、E是圆C上的两个点,且DE垂直于x轴,DE的中点为H,点D(x2,y2),则H(x2,y3),求得|DC|和|CH|、|DH|2,可得当x2=2时,|DH|2=2,故弦长为|DE|=2|DH|=2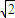 为定值,由此可得结论
为定值,由此可得结论 -2,∴a=
-2,∴a=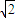 -1,∴b2=c2-a2=2
-1,∴b2=c2-a2=2 -2.
-2.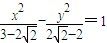 .
.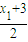 ,
,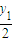 ).
). |AP|=
|AP|=
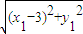 ,|CH|=|
,|CH|=|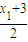 -x2|=
-x2|= |(x1-2x2)+3|,
|(x1-2x2)+3|, [
[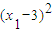 +
+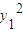 ]-
]-
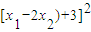 =(x2-2)x1-
=(x2-2)x1-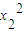 +3x2
+3x2 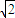 为定值.
为定值.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 | ||
3-2
|
| y2 | ||
2
|
| x2 | ||
3-2
|
| y2 | ||
2
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2009年山东省济宁市高考数学一模试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com