
【题目】国家学生体质健康测试专家组到某学校进行测试抽查,在高三年级随机抽取100名男生参加实心球投掷测试,测得实心球投掷距离(均在5至15米之内)的频数分布表如下(单位:米):
分组 |
|
|
|
|
|
频数 | 9 | 23 | 40 | 22 | 6 |
规定:实心球投掷距离在![]() 之内时,测试成绩为“良好”,以各组数据的中间值代表这组数据的平均值
之内时,测试成绩为“良好”,以各组数据的中间值代表这组数据的平均值![]() ,将频率视为概率.
,将频率视为概率.
(1)求![]() ,并估算该校高三年级男生实心球投掷测试成绩为“良好”的百分比.
,并估算该校高三年级男生实心球投掷测试成绩为“良好”的百分比.
(2)现在从实心球投掷距离在![]() ,
,![]() 之内的男生中用分层抽样的方法抽取5人,再从这5人中随机抽取3人参加提高体能的训练,求:在被抽取的3人中恰有两人的实心球投掷距离在
之内的男生中用分层抽样的方法抽取5人,再从这5人中随机抽取3人参加提高体能的训练,求:在被抽取的3人中恰有两人的实心球投掷距离在![]() 内的概率.
内的概率.
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() .数列
.数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求正整数
,求正整数![]() 的值;
的值;
(2)若数列![]() ,
,![]() 均是等差数列,求
均是等差数列,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,且
,且![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差数列,若存在,求出一个
成等差数列,若存在,求出一个![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
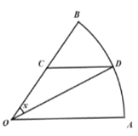
【题目】为庆祝某校一百周年校庆,展示该校一百年来的办学成果及优秀校友风采,学校准备校庆期间搭建一个扇形展览区,如图,是一个半径为2百米,圆心角为![]() 的扇形展示区的平面示意图.点
的扇形展示区的平面示意图.点![]() 是半径
是半径![]() 上一点,点
上一点,点![]() 是圆弧
是圆弧![]() 上一点,且
上一点,且![]() .为了实现“以展养展”,现决定:在线段
.为了实现“以展养展”,现决定:在线段![]() 、线段
、线段![]() 及圆弧
及圆弧![]() 三段所示位置设立广告位,经测算广告位出租收入是:线段
三段所示位置设立广告位,经测算广告位出租收入是:线段![]() 处每百米为
处每百米为![]() 元,线段
元,线段![]() 及圆弧
及圆弧![]() 处每百米均为
处每百米均为![]() 元.设
元.设![]() 弧度,广告位出租的总收入为
弧度,广告位出租的总收入为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)试问![]() 为何值时,广告位出租的总收入最大,并求出其最大值.
为何值时,广告位出租的总收入最大,并求出其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
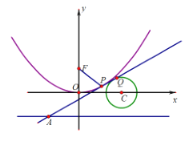
【题目】已知如图,直线![]() 是抛物线
是抛物线![]() (
(![]() )和圆C:
)和圆C:![]() 的公切线,切点(在第一象限)分别为P、Q.F为抛物线的焦点,切线
的公切线,切点(在第一象限)分别为P、Q.F为抛物线的焦点,切线![]() 交抛物线的准线于A,且
交抛物线的准线于A,且![]() .
.
(1)求切线![]() 的方程;
的方程;
(2)求抛物线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆的离心率为
,椭圆的离心率为![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() ,与以右焦点
,与以右焦点![]() 为圆心,半径为
为圆心,半径为![]() 的圆
的圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)线段![]() 是椭圆
是椭圆![]() 过右焦点
过右焦点![]() 的弦,且
的弦,且![]() ,求
,求![]() 的面积的最大值以及取最大值时实数
的面积的最大值以及取最大值时实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数![]()
![]() ,其中
,其中![]() 为虚数单位,对于任意复数
为虚数单位,对于任意复数![]() ,有
,有![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)若复数![]() 满足
满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)我们把上述关系式看作复平面上表示复数![]() 的点
的点![]() 和表示复数
和表示复数![]() 的点
的点![]() 之间的一个变换,问是否存在一条直线
之间的一个变换,问是否存在一条直线![]() ,若点
,若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 仍然在直线
仍然在直线![]() 上?如果存在,求出直线
上?如果存在,求出直线![]() 的方程,否则,说明理由.
的方程,否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机给人们的生活带来便利的同时,也给青少年的成长带来不利的影响,有人沉迷于手机游戏无法自拔,严重影响了自己的学业,某学校随机抽取![]() 个班,调查各班带手机来学校的人数,所得数据的茎叶图如图所示.以组距为
个班,调查各班带手机来学校的人数,所得数据的茎叶图如图所示.以组距为![]() 将数据分组成
将数据分组成![]() ,
,![]() ,…,
,…,![]() ,
,![]() 时,所作的频率分布直方图是( )
时,所作的频率分布直方图是( )

A.  B.
B. 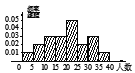
C. 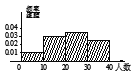 D.
D. 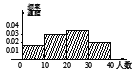
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com