Question

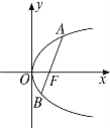
【题目】已知直线l经过抛物线y2＝6x的焦点F，且与抛物线相交于A，B两点．

(1)若直线l的倾斜角为60°，求|AB|的值；

(2)若|AB|＝9，求线段AB的中点M到准线的距离．

Answer 1

【答案】（1）8（2）

【解析】

（1）由y2＝6x，得准线方程、焦点，直线的方程为，与抛物线方程联立可得x2－5x＋＝0，设A(x1，y1)，B(x2，y2)，则x1＋x2＝5，由抛物线的定义可知线段AB的长；

（2），即可求线段AB的中点M到准线的距离．

(1)因为直线l的倾斜角为60°，所以其斜率k＝tan 60°＝．

又F，所以直线l的方程为y＝．

联立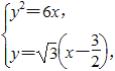消去y得x2－5x＋＝0．设A(x1，y1)，B(x2，y2)，则x1＋x2＝5，

而|AB|＝|AF|＋|BF|＝x1＋＋x2＋＝x1＋x2＋p，所以|AB|＝5＋3＝8．

(2)设A(x1，y1)，B(x2，y2)，由抛物线定义知|AB|＝|AF|＋|BF|＝x1＋x2＋p＝x1＋x2＋3，

所以x1＋x2＝6，于是线段AB的中点M的横坐标是3．又准线方程是x＝－，

所以M到准线的距离为3＋＝．