

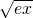 在区间[0,
在区间[0, ]上的定积分,与函数y=-lnx在区间[
]上的定积分,与函数y=-lnx在区间[ ,1]上的定积分的和.再用定积分计算公式加以运算即可得到本题答案.
,1]上的定积分的和.再用定积分计算公式加以运算即可得到本题答案. ,1)
,1)

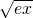 dx+
dx+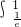 (-lnx)dx
(-lnx)dx )
)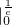 +[x(1-lnx)]
+[x(1-lnx)]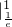
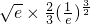 +[1×(1-ln1)-
+[1×(1-ln1)- (1-ln
(1-ln )]
)]



 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com