
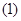 定义在
定义在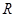 上;
上;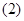 存在
存在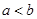 ,使其在
,使其在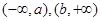 上单调递增,在
上单调递增,在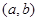 上单调递减,则以下函数是“好函数”的有 .
上单调递减,则以下函数是“好函数”的有 .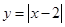 ;?
;?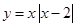 ;?
;?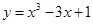 ;④
;④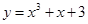
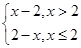 ∴不存在a,使y=|x-2|在(-∞,a)上单调递增,故不正确;②中函数y=x|x-2|定义域为R,y=x|x-2|=
∴不存在a,使y=|x-2|在(-∞,a)上单调递增,故不正确;②中函数y=x|x-2|定义域为R,y=x|x-2|=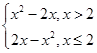 y=x|x-2|在(-∞,1)、(2,+∞)上单调递增,在(1,2)上单调递减,满足好函数的定义,故正确;③中函数y=x3-x+1定义域为R,则y′=3x2-1<0解得x∈(-
y=x|x-2|在(-∞,1)、(2,+∞)上单调递增,在(1,2)上单调递减,满足好函数的定义,故正确;③中函数y=x3-x+1定义域为R,则y′=3x2-1<0解得x∈(-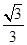 ,
,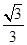 ),y′=3x2-1>0解得x∈(-∞,-
),y′=3x2-1>0解得x∈(-∞,-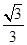 )∪(
)∪(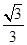 ,+∞),∴y=x3-x+1在(-∞,-
,+∞),∴y=x3-x+1在(-∞,-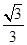 )、(
)、(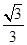 ,+∞)上单调递增,在(-
,+∞)上单调递增,在(-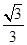 ,
,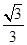 )上单调递减,满足好函数的定义,故正确;④中函数y=x3+x+3定义域为R,则y′=3x2+1>0恒成立,故不存在a<b,使函数y=x3+x+3在(a,b)上单调递减,不满足好函数的定义,故不正确;故答案为:②③
)上单调递减,满足好函数的定义,故正确;④中函数y=x3+x+3定义域为R,则y′=3x2+1>0恒成立,故不存在a<b,使函数y=x3+x+3在(a,b)上单调递减,不满足好函数的定义,故不正确;故答案为:②③

 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 万元满足
万元满足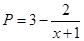 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为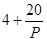 元.
元.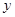 万元表示为促销费用
万元表示为促销费用 万元的函数;
万元的函数;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com