
【题目】某公司生产某种产品,一条流水线年产量为![]() 件,该生产线分为两段,流水线第一段生产的半成品的质量指标会影响第二段生产成品的等级,具体见下表:
件,该生产线分为两段,流水线第一段生产的半成品的质量指标会影响第二段生产成品的等级,具体见下表:
第一段生产的半成品质量指标 |
|
|
|
第二段生产的成品为一等品概率 | 0.2 | 0.4 | 0.6 |
第二段生产的成品为二等品概率 | 0.3 | 0.3 | 0.3 |
第二段生产的成品为三等品概率 | 0.5 | 0.3 | 0.1 |
从第一道生产工序抽样调查了![]() 件,得到频率分布直方图如图:
件,得到频率分布直方图如图:

若生产一件一等品、二等品、三等品的利润分别是![]() 元、
元、![]() 元、
元、![]() 元.
元.
(Ⅰ)以各组的中间值估计为该组半成品的质量指标,估算流水线第一段生产的半成品质量指标的平均值;
(Ⅱ)将频率估计为概率,试估算一条流水线一年能为该公司创造的利润;
(Ⅲ)现在市面上有一种设备可以安装到流水线第一段,价格是![]() 万元,使用寿命是
万元,使用寿命是![]() 年,安装这种设备后,流水线第一段半成品的质量指标服从正态分布
年,安装这种设备后,流水线第一段半成品的质量指标服从正态分布![]() ,且不影响产量.请你帮该公司作出决策,是否要购买该设备?说明理由.
,且不影响产量.请你帮该公司作出决策,是否要购买该设备?说明理由.
(参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 万元;(Ⅲ)见解析.
万元;(Ⅲ)见解析.
【解析】
(Ⅰ)首先根据频率分布直方图确定各组的频率及中间值,再根据样本平均数的计算公式计算得到平均数;(Ⅱ)首先确定随机变量![]() 的所有可能取值,再根据独立事件的概率公式求出分布列,最后利用数学期望公式求
的所有可能取值,再根据独立事件的概率公式求出分布列,最后利用数学期望公式求![]() 的数学期望;(Ⅲ)首先根据正态分布的性质确定好
的数学期望;(Ⅲ)首先根据正态分布的性质确定好![]() 等,然后类似第二问求出随机变量
等,然后类似第二问求出随机变量![]() 的分布列及数学期望,最后根据随机变量
的分布列及数学期望,最后根据随机变量![]() 的数学期望的大小作决策.
的数学期望的大小作决策.
(Ⅰ)平均值为:![]() .
.
(Ⅱ)由频率直方图,第一段生产半成品质量指标![]() 或
或![]()
![]() ,
,
![]() 或
或![]()
![]() ,
,![]() ,
,
设生产一件产品的利润为![]() 元,则
元,则
![]()
![]() ,
,
![]() ,
,
![]() ,
,
所以生产一件成品的平均利润是![]() 元,
元,
所以一条流水线一年能为该公司带来利润的估计值是![]() 万元.
万元.
(Ⅲ)![]() ,
,
设引入该设备后生产一件成品利润为![]() 元,则
元,则
![]() ,
,
![]() ,
,
![]() ,
,
所以引入该设备后生产一件成品平均利润为
![]() 元,
元,
所以引入该设备后一条流水线一年能为该公司带来利润的估计值是![]() 万元,
万元,
增加收入![]() 万元,
万元,
综上,应该引入该设备.


科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 的底面边长和高都为2.现从该棱锥的5个顶点中随机选取3个点构成三角形,设随机变量
的底面边长和高都为2.现从该棱锥的5个顶点中随机选取3个点构成三角形,设随机变量![]() 表示所得三角形的面积.
表示所得三角形的面积.
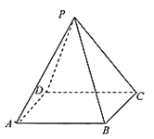
(1)求概率![]() 的值;
的值;
(2)求随机变量![]() 的概率分布及其数学期望
的概率分布及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑。若三棱锥P-ABC为鳖臑,PA⊥面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球的球面上,则球0的表面积为( )
A. 8πB. 12πC. 20πD. 24π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究机构对某校学生往返校时间的统计资料表明:该校学生居住地到学校的距离![]() (单位:千米)和学生花费在上学路上的时间
(单位:千米)和学生花费在上学路上的时间![]() (单位:分钟)有如下的统计资料:
(单位:分钟)有如下的统计资料:
到学校的距离 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花费的时间 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明![]() 与
与![]() 有线性相关关系,试求:
有线性相关关系,试求:
(1)判断![]() 与
与![]() 是否有很强的线性相关性?
是否有很强的线性相关性?
(相关系数![]() 的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
(2)求线性回归方程![]() (精确到0.01);
(精确到0.01);
(3)将![]() 分钟的时间数据
分钟的时间数据![]() 称为美丽数据,现从这6个时间数据
称为美丽数据,现从这6个时间数据![]() 中任取2个,求抽取的2个数据全部为美丽数据的概率.
中任取2个,求抽取的2个数据全部为美丽数据的概率.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
参考公式: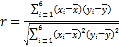 ,
,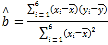
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,
,![]() ,若
,若![]() ,
,![]() ,则称
,则称![]() 是
是![]() 的“收缩数列”.其中
的“收缩数列”.其中![]() ,
,![]() 分别表示
分别表示![]() 中的最大数和最小数.已知
中的最大数和最小数.已知![]() 为无穷数列,其前
为无穷数列,其前![]() 项和为
项和为![]() ,数列
,数列![]() 是
是![]() 的“收缩数列”.
的“收缩数列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 项和;
项和;
(2)证明:![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() ;
;
(3)若![]() 且
且![]() ,
,![]() ,求所有满足该条件的
,求所有满足该条件的![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动眯,当
上的一个动眯,当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离的最小值;
的距离的最小值;
(2)若曲线![]() 上所有的点都在直线
上所有的点都在直线![]() 的右下方,求实数
的右下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,D是边AC上的一点,将
,D是边AC上的一点,将![]() 沿BD折叠,得到三棱锥
沿BD折叠,得到三棱锥![]() ,若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设
,若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设![]() ,则x的取值范围是( )
,则x的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com