Question

【题目】在中，已知，，D是边AC上的一点，将沿BD折叠，得到三棱锥，若该三棱锥的顶点A在底面BCD的射影M在线段BC上，设，则x的取值范围是（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

由题意可得，折叠前在图1中，AM⊥BD垂足为N.设图1中A点在BC上的射影为M1，运动点D可得，当D点与C点无限接近时，点M与点M1无限接近，得到BM＞BM1.在图2中，根据斜边大于直角边，可得BM＜AB，由此可得x的取值范围.

将△ABD沿BD折起，得到三棱锥A-BCD，且点A在底面BCD的射影M在线段BC上，

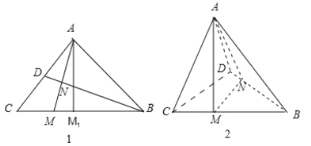
如图2，AM⊥平面BCD，则AM⊥BD，过M作MN⊥BD，连接AN，则AN⊥BD，

因此，折叠前在图1中，AM⊥BD，垂足为N.

在图1中，过A作AM1⊥BC于M1，运动点D，当D点与C点无限接近时，折痕BD接近BC，此时M与点M1无限接近；

在图2中，由于AB是Rt△ABM的斜边，BM是直角边，因此BM＜AB

由此可得:BM1＜BM＜AB

因为△ABC中，AB＝2，BC＝2，∠ABC＝45°，由余弦定理可得AC＝2，

B M1＝

故选：C