
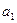 ,
,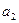 ,…,
,…, ,
, ,
,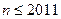 .(注:框图中的赋值符号“
.(注:框图中的赋值符号“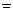 ”也可以写成“
”也可以写成“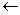 ”或“:
”或“: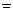 ”)
”) ,写出输出结果;
,写出输出结果;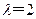 ,求数列
,求数列 的通项公式;
的通项公式; ,令
,令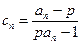 ,求常数
,求常数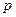 (
(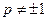 ),使得
),使得 是等比数列.
是等比数列.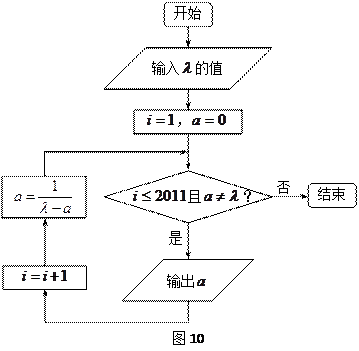
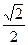 ,
,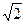 .……3分
.……3分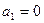 ,
,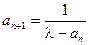 ,
, ,
,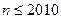 .
.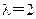 时,
时,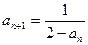 , …………………5分
, …………………5分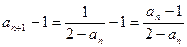 ,而
,而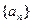 中的任意一项均不为1,(否则的话,由
中的任意一项均不为1,(否则的话,由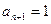 可以得到
可以得到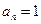 ,…,与
,…,与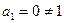 矛盾),
矛盾),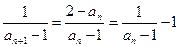 ,
,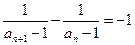 (常数),
(常数), ,
,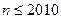 .故
.故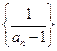 是首项为
是首项为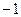 ,公差为
,公差为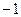 的等差数列, ……………………………7分
的等差数列, ……………………………7分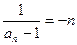 ,数列
,数列 的通项公式为
的通项公式为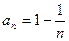 ,
, ,
,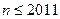 .…8分
.…8分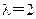 时,由程序框图可知,
时,由程序框图可知,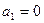 ,
,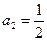 ,
,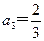 ,
,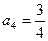 ,……
,……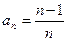 ,
, ,
,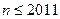 . …………………………………………5分
. …………………………………………5分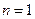 时,
时,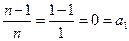 ,猜想正确;
,猜想正确;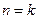 (
( ,
,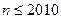 )时,猜想正确.即
)时,猜想正确.即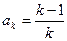 ,………………7分
,………………7分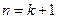 时,
时,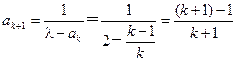 .即
.即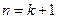 时,猜想也正确.
时,猜想也正确.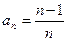 正确,
正确, ,
,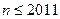 .……8分
.……8分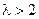 时,
时,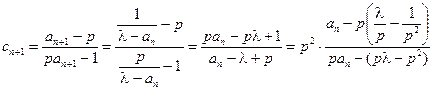 ,
,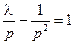 ,则
,则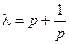 ,
,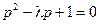 ,
,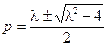 . …………10分
. …………10分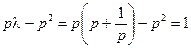 , ………………………………12分
, ………………………………12分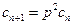 ,
, ,
,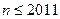 ,又
,又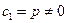 ,
,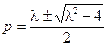 (
(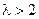 ),
), 是以
是以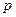 为首项,
为首项,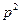 为公比的等比数列. ……………………………14分
为公比的等比数列. ……………………………14分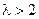 时,令
时,令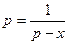 ,即
,即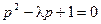 ,解得
,解得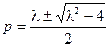 ,…10分
,…10分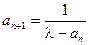 ,
, ,
,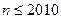 .
.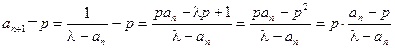 , ①
, ①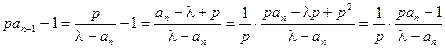 ,② 12分
,② 12分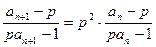 ,
,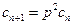 ,
, ,
,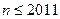 ,又
,又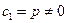 ,
,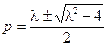 (
(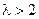 )
) 是以
是以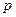 为首项,
为首项,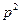 为公比的等比数列. ……………………………14分
为公比的等比数列. ……………………………14分

科目:高中数学 来源:不详 题型:解答题
 1=c,2Sn=anan+1+r.
1=c,2Sn=anan+1+r. 满足的条件;若不能,请说明理由.
满足的条件;若不能,请说明理由. ,
, ,
,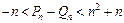 恒成立.
恒成立.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 0年举办第四届),下表列出了1974年联邦德国第十届世界杯足球赛以来的几届世界杯举办地:
0年举办第四届),下表列出了1974年联邦德国第十届世界杯足球赛以来的几届世界杯举办地:| 年份 | 1974 | 1978 | 1982 | … | 2006 |
| 举办地 | 联邦德国 | 阿根廷 | 西班牙 | … | 德国 |
A. 18 18 | B.19 | C.20 | D.21 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
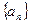 、
、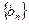 都是等
都是等 差数列,且
差数列,且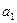 =5,
=5,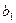 =15,
=15,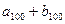 =100,则数列
=100,则数列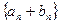 的前
的前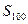 等于: ( )
等于: ( ) 、 6000 D、60000
、 6000 D、60000查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com