
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,且
,且![]() 过点
过点![]() ,圆
,圆![]() 是以线段
是以线段![]() 为直径的圆,经过点
为直径的圆,经过点![]() 且倾斜角为
且倾斜角为![]() 的直线与圆
的直线与圆![]() 相切.
相切.
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相切,与椭圆
相切,与椭圆![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ?若存在,请求出直线
?若存在,请求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
【答案】(1)椭圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ;(2)不存在
;(2)不存在
【解析】分析:(1)由题意得![]() ,再根据椭圆过点
,再根据椭圆过点![]() 得到关于
得到关于![]() 的方程组,求解后可得椭圆和圆的方程.(2)先假设存在直线满足条件.(ⅰ)当直线斜率不存在时,可得直线方程为
的方程组,求解后可得椭圆和圆的方程.(2)先假设存在直线满足条件.(ⅰ)当直线斜率不存在时,可得直线方程为![]() ,求得点
,求得点![]() 的坐标后验证可得
的坐标后验证可得![]() ;(ⅱ)当直线斜率存在时,设出直线方程,与椭圆方程联立消元后得到一元二次方程,结合根据系数的关系可得
;(ⅱ)当直线斜率存在时,设出直线方程,与椭圆方程联立消元后得到一元二次方程,结合根据系数的关系可得
![]() 不成立.从而可得不存在直线
不成立.从而可得不存在直线![]() 满足题意.
满足题意.
详解:(1)由题意知![]() ,
,![]() ,
,![]() ,圆
,圆![]() 的方程为
的方程为![]()
由题可知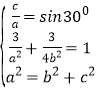 ,解得
,解得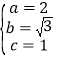 ,
,
所以椭圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.
(2)假设存在直线![]() 满足题意.
满足题意.
由![]() ,可得
,可得![]() ,故
,故![]() .
.
(ⅰ)当直线![]() 的斜率不存在时,此时
的斜率不存在时,此时![]() 的方程为
的方程为![]() .
.
当直线![]() 时,可得
时,可得![]()
所以![]() .
.
同理可得,当![]() 时,
时,![]() .
.
故直线![]() 不存在.
不存在.
(ⅱ)当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 方程为
方程为![]() ,
,
因为直线![]() 与圆
与圆![]() 相切,
相切,
所以![]() ,整理得
,整理得![]() ①
①
由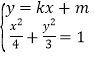 消去y整理得
消去y整理得![]() ,
,
设![]() ,
,
则![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() ,
,
则![]() ,即
,即![]() ,
,
所以![]() ,
,
所以![]() ,
,
整理得![]() ②
②
由①②得![]() ,此时方程无解.
,此时方程无解.
故直线![]() 不存在.
不存在.
由(i)(ii)可知不存在直线![]() 满足题意.
满足题意.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
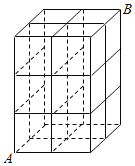
【题目】如图,某建筑工地搭建的脚手架局部类似于一个![]() 的长方体框架,一个建筑工人欲从
的长方体框架,一个建筑工人欲从![]() 处沿脚手架攀登至
处沿脚手架攀登至 ![]() 处,则其最近的行走路线中不连续向上攀登的概率为( )
处,则其最近的行走路线中不连续向上攀登的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数![]() (
(![]() ,
,![]() ),关于
),关于![]() 的不等式
的不等式![]() 的解集中有且只有一个元素.
的解集中有且只有一个元素.
(1)设数列![]() 的前
的前![]() 项和
项和![]() (
(![]() ),求数列
),求数列![]() 的通项公式;
的通项公式;
(2)设![]() (
(![]() ),则数列
),则数列![]() 中是否存在不同的三项能组成等比数列?请说明理由.
中是否存在不同的三项能组成等比数列?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:①“若![]() ,则
,则![]() ,
,![]() 互为倒数”的逆命题;②“面积相等的三角形全等”的否命题;③“若
互为倒数”的逆命题;②“面积相等的三角形全等”的否命题;③“若![]() ,则
,则![]() 有实数解”的逆否命题;④“若
有实数解”的逆否命题;④“若![]() ,则
,则![]() ”的逆否命题.其中真命题为________(填写所有真命题的序号).
”的逆否命题.其中真命题为________(填写所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且经过点
,且经过点![]() ,直线
,直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() .
.
(1)求椭圆的方程;
(2)求![]() 的取值范围;
的取值范围;
(3)若直线![]() 不过点
不过点![]() ,求证:直线
,求证:直线![]() 的斜率互为相反数.
的斜率互为相反数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场去年国庆期间累计生成![]() 万张购物单,从中随机抽出
万张购物单,从中随机抽出![]() 张,对每单消费金额进行统计得到下表:
张,对每单消费金额进行统计得到下表:
消费金额(单位:元) |
|
|
|
|
|
购物单张数 | 25 | 25 | 30 |
由于工作人员失误,后两栏数据无法辨识,但当时记录表明,根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等.用频率估计概率,完成下列问题:
(1)估计去年国庆期间该商场累计生成的购物单中,单笔消费额超过![]() 元的概率;
元的概率;
(2)为鼓励顾客消费,该商场计划在今年国庆期间进行促销活动,凡单笔消费超过![]() 元者,可抽奖一次.抽奖规则为:从装有大小材质完全相同的
元者,可抽奖一次.抽奖规则为:从装有大小材质完全相同的![]() 个红球和
个红球和![]() 个黑球的不透明口袋中,随机摸出
个黑球的不透明口袋中,随机摸出![]() 个小球,并记录两种颜色小球的数量差的绝对值
个小球,并记录两种颜色小球的数量差的绝对值![]() ,当
,当![]() 时,消费者可分别获得价值
时,消费者可分别获得价值![]() 元、
元、![]() 元和
元和![]() 元的购物券.求参与抽奖的消费者获得购物券的价值的数学期望.
元的购物券.求参与抽奖的消费者获得购物券的价值的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,杨老师的微信朋友圈内有
推出的多款健康运动软件中的一款,杨老师的微信朋友圈内有![]() 位好友参与了“微信运动”,他随机选取了
位好友参与了“微信运动”,他随机选取了![]() 位微信好友(女
位微信好友(女![]() 人,男
人,男![]() 人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
5860 8520 7326 6798 7325 8430 3216 7453 11754 9860
8753 6450 7290 4850 10223 9763 7988 9176 6421 5980
男性好友走路的步数情况可分为五个类别: ![]() 步)(说明:“
步)(说明:“![]() ”表示大于等于
”表示大于等于![]() ,小于等于
,小于等于![]() .下同),
.下同), ![]() 步),
步), ![]() 步),
步), ![]() 步),
步), ![]() 步及以
步及以![]() ),且
),且![]() 三种类别人数比例为
三种类别人数比例为![]() ,将统计结果绘制如图所示的条形图.
,将统计结果绘制如图所示的条形图.

若某人一天的走路步数超过![]() 步被系统认定为“卫健型",否则被系统认定为“进步型”.
步被系统认定为“卫健型",否则被系统认定为“进步型”.
(1)若以杨老师选取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计杨老师的微信好友圈里参与“微信运动”的![]() 名好友中,每天走路步数在
名好友中,每天走路步数在![]() 步的人数;
步的人数;
(2)请根据选取的样本数据完成下面的![]() 列联表并据此判断能否有
列联表并据此判断能否有![]() 以上的把握认定“认定类型”与“性别”有关?
以上的把握认定“认定类型”与“性别”有关?
| p> | 卫健型 | 进步型 | 总计 |
男 | 20 | ||
女 | 20 | ||
总计 | 40 |
(3)若从杨老师当天选取的步数大于10000的好友中按男女比例分层选取![]() 人进行身体状况调查,然后再从这
人进行身体状况调查,然后再从这![]() 位好友中选取
位好友中选取![]() 人进行访谈,求至少有一位女性好友的概率.
人进行访谈,求至少有一位女性好友的概率.
附:  ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com