
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点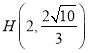 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)点![]() 在圆
在圆![]() 上,且
上,且![]() 在第一象限,过
在第一象限,过![]() 作
作![]() 的切线交椭圆于
的切线交椭圆于![]() 两点,问:
两点,问: ![]() 的周长是否为定值?若是,求出定值;若不是,说明理由.
的周长是否为定值?若是,求出定值;若不是,说明理由.
科目:高中数学 来源: 题型:
【题目】设点![]() ,满足|PA|=2|PB|的点
,满足|PA|=2|PB|的点![]() 的轨迹是圆M:x2+y2
的轨迹是圆M:x2+y2![]() x+Ey+F=0.直线AB与圆M相交于C,D两点,
x+Ey+F=0.直线AB与圆M相交于C,D两点,![]() ,且点C的纵坐标为
,且点C的纵坐标为![]() .
.
(1)求a,b的值;
(2)已知直线l:x+y+2=0与圆M相交于G,H两点,求|GH|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他民俗活动的民间艺术;蕴含了极致的数学美和丰富的传统文化信息,现有一幅剪纸的设计图,其中的4个小圆均过正方形的中心,且内切于正方形的两邻边.若在正方形内随机取一点,则该点取自黑色部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与
与![]() 轴相切,且与圆
轴相切,且与圆![]() :
:![]() 外切;
外切;
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若直线![]() 过定点
过定点![]() ,且与轨迹
,且与轨迹![]() 交于
交于![]() 、
、![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 、
、![]() 两点,若点
两点,若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求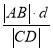 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)若![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动,组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后,学生会对问卷结果进行了统计,并将其中一个问题“是否知道垃圾分类方法(知道或不知道)”的调查结果统计如下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
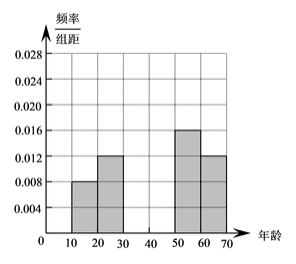
(1)求上表中的![]() 的值,并补全右图所示的的频率直方图;
的值,并补全右图所示的的频率直方图;
(2)在被调查的居民中,若从年龄在![]() 的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率
的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一项针对某一线城市30~50岁都市中年人的消费水平进行调查,现抽查500名(200名女性,300名男性)此城市中年人,最近一年内购买六类高价商品(电子产品、服装、手表、运动与户外用品、珠宝首饰、箱包)的金额(万元)的频数分布表如下:
女性 | 金额 |
|
|
|
|
|
频数 | 20 | 40 | 80 | 50 | 10 | |
男性 | 金额 |
|
|
|
|
|
频数 | 45 | 75 | 90 | 60 | 30 |
(1)将频率视为概率,估计该城市中年人购买六类高价商品的金额不低于5000元的概率.
(2)把购买六类高价商品的金额不低于5000元的中年人称为“高收入人群”,根据已知条件完成![]() 列联表,并据此判断能否有95%的把握认为“高收入人群”与性别有关?
列联表,并据此判断能否有95%的把握认为“高收入人群”与性别有关?
高收入人群 | 非高收入人群 | 合计 | |
女性 | 60 | ||
男性 | 180 | ||
合计 | 500 |
参考公式: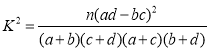 ,其中
,其中![]()
参考附表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 在第一象限内的点
在第一象限内的点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() .
.
(1)若![]() ,过点
,过点![]() ,
, ![]() 的直线
的直线![]() 与抛物线相交于另一点
与抛物线相交于另一点![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,与圆
两点,与圆![]() 相交于
相交于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得
,使得![]() 的长为定值?若存在,求出
的长为定值?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com