
| A. | $\sqrt{3}$d,$\frac{{\sqrt{3}}}{3}$d | B. | $\frac{{\sqrt{3}}}{3}$d,$\frac{{\sqrt{6}}}{3}$d | C. | $\frac{{\sqrt{6}}}{3}$d,$\frac{{\sqrt{3}}}{3}$d | D. | $\frac{{\sqrt{6}}}{3}$d,$\sqrt{3}$d |
分析 据题意横梁的强度同它的断面高的平方与宽x的积成正比(强度系数为k,k>0)建立起强度函数,求出函数的定义域,再利用求导的方法求出函数取到最大值时的横断面的值.
解答 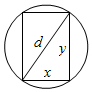 解:如图所示,设矩形横断面的宽为x,高为y.由题意知,当xy2取最大值时,横梁的强度最大.
解:如图所示,设矩形横断面的宽为x,高为y.由题意知,当xy2取最大值时,横梁的强度最大.
∵y2=d2-x2,
∴xy2=x(d2-x2)(0<x<d).
令f(x)=x(d2-x2)(0<x<d),
得f′(x)=d2-3x2,令f′(x)=0,
解得x=$\frac{\sqrt{3}}{3}$d或x=-$\frac{\sqrt{3}}{3}$d(舍去).
当0<x<$\frac{\sqrt{3}}{3}$d,f′(x)>0;当$\frac{\sqrt{3}}{3}$d<x<d时,f′(x)<0,
因此,当x=$\frac{\sqrt{3}}{3}$d时,f(x)取得极大值,也是最大值.
∴y=$\frac{\sqrt{6}}{3}$d
故选:C.
点评 考查据实际意义建立相关的函数,再根据函数的特征选择求导的方法来求最值.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:解答题
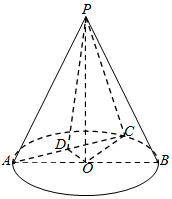 如图所示在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$上的点(点C不与AB重合),D为AC中点.
如图所示在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$上的点(点C不与AB重合),D为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2<b2 | B. | $\frac{b}{a}>1$ | C. | lg(b-a)>0 | D. | ($\frac{1}{3}$)a>($\frac{1}{3}$)b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
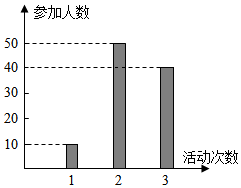 某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y-2)2=5 | B. | (x+1)2+(y+2)2=5 | C. | (x-1)2+(y-2)2=3 | D. | (x+1)2+(y+2)2=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com