
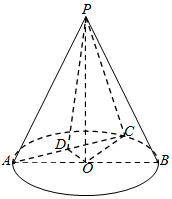
 如图所示在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$上的点(点C不与AB重合),D为AC中点.
如图所示在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$上的点(点C不与AB重合),D为AC中点.分析 (Ⅰ)根据△AOC是等腰直角三角形证出中线OD⊥AC,再结合PD⊥AC证出AC⊥POD,利用平面与平面垂直的判定定理,可证出平面POD⊥平面PAC;
(Ⅱ)求出母线,即可求圆锥PO的表面积.
解答 (Ⅰ)证明:∵PA=PD,D是AC中点,
∴PD⊥AC.…(2分)
又∵OA=OC,D是AC中点,
∴OD⊥AC.…(4分)
又∵PD、OD?平面POD,且PD∩OD=D,
∴AC⊥平面POD.…(6分)
∴平面POD⊥平面PAC.…(8分)
(Ⅱ)解:∵$PO=\sqrt{2}$,底面半径$r=OB=\frac{1}{2}AB=1$,∴母线$l=PB=\sqrt{2+1}=\sqrt{3}$
∴表面积$S=π{r^2}+πrl=π×1+π×1×\sqrt{3}=({1+\sqrt{3}})π$.…(12分)
点评 本题考查直线与平面垂直、平面与平面垂直的证明,考查表面积的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
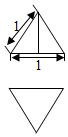 已知某三棱锥的正视图和俯视图如图所示,则此三棱锥的体积为( )
已知某三棱锥的正视图和俯视图如图所示,则此三棱锥的体积为( )| A. | $\frac{{\sqrt{2}}}{12}$ | B. | $\frac{{\sqrt{3}}}{12}$ | C. | $\frac{1}{8}$ | D. | $\frac{{\sqrt{3}}}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$d,$\frac{{\sqrt{3}}}{3}$d | B. | $\frac{{\sqrt{3}}}{3}$d,$\frac{{\sqrt{6}}}{3}$d | C. | $\frac{{\sqrt{6}}}{3}$d,$\frac{{\sqrt{3}}}{3}$d | D. | $\frac{{\sqrt{6}}}{3}$d,$\sqrt{3}$d |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{25}$ | B. | $-\frac{24}{25}$ | C. | $\frac{7}{25}$ | D. | $-\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解班级学生对任课教师课堂教学的满意程度情况.现从某班全体学生中,随机抽取12名,测试的满意度分数(百分制)如茎叶图所示:
为了解班级学生对任课教师课堂教学的满意程度情况.现从某班全体学生中,随机抽取12名,测试的满意度分数(百分制)如茎叶图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com