
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
分析 (1)利用描点法可得图象;
(2)根据所给的数据,做出变量x,y的平均数,再求出a,b的值,即可求线性回归方程;
(3)当自变量为10时,代入线性回归方程,求出维修费用,这是一个预报值.
解答 解:(1)作散点图如下: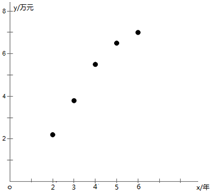
由散点图可知是线性相关的…(3分)
(2)根据题意列表如下:
| i | 1 | 2 | 3 | 4 | 5 |
| xi | 2 | 3 | 4 | 5 | 6 |
| yi | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| xiyi | 4.4 | 11.4 | 22.0 | 32.5 | 42.0 |
| $\overline{x}$=4,$\overline{y}$=5,$\sum_{i=1}^{5}{{x}_{i}}^{2}$=90,$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=112.3 | |||||
点评 本题考查线性回归方程的求解和应用,是一个基础题,解题的关键是正确应用最小二乘法来求线性回归方程的系数.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
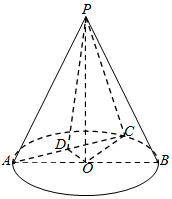 如图所示在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$上的点(点C不与AB重合),D为AC中点.
如图所示在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$上的点(点C不与AB重合),D为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
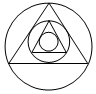 记半径为1的圆为C1,C1的外切正三角形的外接圆为C2,C2的外切正三角形的外接圆C3,…Cn-1的外切正三角形的外接圆为Cn,则C16的面积是( )
记半径为1的圆为C1,C1的外切正三角形的外接圆为C2,C2的外切正三角形的外接圆C3,…Cn-1的外切正三角形的外接圆为Cn,则C16的面积是( )| A. | 215•π | B. | 216•π | C. | 230•π | D. | 232•π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y-2)2=5 | B. | (x+1)2+(y+2)2=5 | C. | (x-1)2+(y-2)2=3 | D. | (x+1)2+(y+2)2=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com