
| A. | $\frac{24}{25}$ | B. | $-\frac{24}{25}$ | C. | $\frac{7}{25}$ | D. | $-\frac{7}{25}$ |
分析 法一:利用特殊角的三角函数值,两角和的正弦函数公式展开已知可求sinx+cosx=$\frac{3\sqrt{2}}{5}$,两边平方可得sin2x=-$\frac{7}{25}$,结合已知可求范围2x∈(π,$\frac{3π}{2}$),利用同角三角函数基本关系式即可求得cos2x的值;
法二:由已知可求cos(x+$\frac{π}{4}$),利用诱导公式,二倍角公式即可计算得解.
解答 解:法一:∵sin(x+$\frac{π}{4}$)=$\frac{3}{5}$,
∴$\frac{\sqrt{2}}{2}$(sinx+cosx)=$\frac{3}{5}$,可得:sinx+cosx=$\frac{3\sqrt{2}}{5}$,
∴平方可得:1+sin2x=$\frac{18}{25}$,解得:sin2x=-$\frac{7}{25}$.
∵0<x<π,可得x+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{5π}{4}$),sin(x+$\frac{π}{4}$)=$\frac{3}{5}$>0,
∴x+$\frac{π}{4}$∈($\frac{π}{4}$,π),可得:x∈(0,$\frac{3π}{4}$),
∴2x∈(0,$\frac{3π}{2}$),
∴结合sin2x=-$\frac{7}{25}$<0,可得:2x∈(π,$\frac{3π}{2}$),
∴cos2x=-$\sqrt{1-si{n}^{2}2x}$=-$\sqrt{1-(-\frac{7}{25})^{2}}$=-$\frac{24}{25}$.
法二:∵0<x<π,可得:x+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{5π}{4}$),
∵sin(x+$\frac{π}{4}$)=$\frac{3}{5}$,
∴利用正弦函数的图象可知必有cos(x+$\frac{π}{4}$)=-$\frac{4}{5}$.
∴cos2x=2sin(x+$\frac{π}{4}$)cos(x+$\frac{π}{4}$)=2×$\frac{3}{5}×(-\frac{4}{5})$=-$\frac{24}{25}$.
故选:B.
点评 本题主要考查了特殊角的三角函数值,两角和的正弦函数公式,同角三角函数基本关系式在三角函数化简求值中的应用,由题意求得范围2x∈(π,$\frac{3π}{2}$)是解题的关键,属于中档题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:解答题
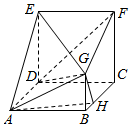 在多面体ABCDEFG中,四边形ABCD与CDEF均为正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.
在多面体ABCDEFG中,四边形ABCD与CDEF均为正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
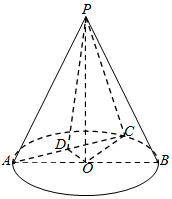 如图所示在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$上的点(点C不与AB重合),D为AC中点.
如图所示在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$上的点(点C不与AB重合),D为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2<b2 | B. | $\frac{b}{a}>1$ | C. | lg(b-a)>0 | D. | ($\frac{1}{3}$)a>($\frac{1}{3}$)b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com