
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 函数f(x),如图所示,[f(x)]2+af(x)<0,当a>0时,-a<f(x)<0.由于关于x的不等式[f(x)]2+af(x)<0恰有1个整数解,因此其整数解为4,f(3)=0.可得f(5)≤-a,-a<f(4)<0,解出即可得出.
解答  解:函数f(x),如图所示,
解:函数f(x),如图所示,
[f(x)]2+af(x)<0,
当a>0时,-a<f(x)<0,
由于关于x的不等式[f(x)]2+af(x)<0恰有1个整数解,
因此其整数解为4,又f(5)=-52+3×5=-10.
f(4)=-42+3×4=-4,f(3)=-32+3×3=0.
∴f(5)≤-a,-a<f(4)<0.
则10≥a>4,
a≤0不必考虑,
可得:实数a的最大值是10.
故选:B.
点评 本题考查了函数的图象与性质、不等式的解法,考查了推理能力与计算能力,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
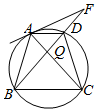 如图所示,四边形ABCD中,AD∥BC,AB=CD,AC,BD交于点Q,∠BAC=∠CAD,AP为四边形ABCD外接圆的切线,交BD的延长线于点P.
如图所示,四边形ABCD中,AD∥BC,AB=CD,AC,BD交于点Q,∠BAC=∠CAD,AP为四边形ABCD外接圆的切线,交BD的延长线于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
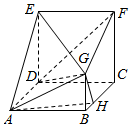 在多面体ABCDEFG中,四边形ABCD与CDEF均为正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.
在多面体ABCDEFG中,四边形ABCD与CDEF均为正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
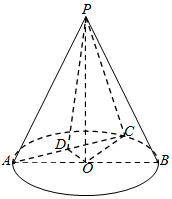 如图所示在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$上的点(点C不与AB重合),D为AC中点.
如图所示在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$上的点(点C不与AB重合),D为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
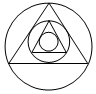 记半径为1的圆为C1,C1的外切正三角形的外接圆为C2,C2的外切正三角形的外接圆C3,…Cn-1的外切正三角形的外接圆为Cn,则C16的面积是( )
记半径为1的圆为C1,C1的外切正三角形的外接圆为C2,C2的外切正三角形的外接圆C3,…Cn-1的外切正三角形的外接圆为Cn,则C16的面积是( )| A. | 215•π | B. | 216•π | C. | 230•π | D. | 232•π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com