
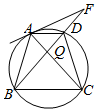
 如图所示,四边形ABCD中,AD∥BC,AB=CD,AC,BD交于点Q,∠BAC=∠CAD,AP为四边形ABCD外接圆的切线,交BD的延长线于点P.
如图所示,四边形ABCD中,AD∥BC,AB=CD,AC,BD交于点Q,∠BAC=∠CAD,AP为四边形ABCD外接圆的切线,交BD的延长线于点P.分析 (1)推导出AB=BC=DC,∠BAC=∠CBD,∠AQP=∠BAC+∠ABQ,∠PAQ=∠ABC=∠ABQ+∠CBD,从而∠PAQ=∠PQA,进而PA=PQ,由此利用切割线能证明PQ2=PA2=PD•PB.
(2)由∠ABP=∠PAD,∠APB=∠APD,得△ABP∽△APD,从而$\frac{AB}{AD}=\frac{AP}{PD}$,求出PD,由此能求出AQ=DQ=PQ-PD,从而能求出结果.
解答 证明:(1)四边形ABCD中,AD∥BC,AB=CD,AC,BD交于点Q,∠BAC=∠CAD,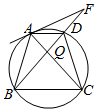
∴AB=BC=DC,∴∠BAC=∠CBD,
∴∠AQP=∠BAC+∠ABQ,
∵AP为四边形ABCD外接圆的切线,交BD的延长线于点P,
∴∠PAQ=∠ABC=∠ABQ+∠CBD,
∴∠PAQ=∠PQA,
∴PA=PQ,
∴PQ2=PA2=PD•PB.
解:(2)∵AB=3,AP=2,AD=$\frac{4}{3}$,AD∥BC,AB=CD,AC,BD交于点Q,∠BAC=∠CAD,
AP为四边形ABCD外接圆的切线,交BD的延长线于点P,
PQ2=PA2=PD•PB
∴PQ2=4=PD•PB,∠ABP=∠PAD,∠APB=∠APD,
∴△ABP∽△APD,∴$\frac{AB}{AD}=\frac{AP}{PD}$,
∴PD=$\frac{AP•AD}{AB}$=$\frac{2×\frac{4}{3}}{3}$=$\frac{8}{9}$,
∴AQ=DQ=PQ-PD=2-$\frac{8}{9}$=$\frac{10}{9}$.
点评 本题考查圆中线段间等量关系的证明,考查线段长的求法,是中档题,解题时要认真审题,注意切割线定理、弦切角定理的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
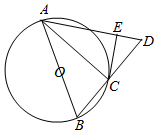 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
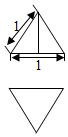 已知某三棱锥的正视图和俯视图如图所示,则此三棱锥的体积为( )
已知某三棱锥的正视图和俯视图如图所示,则此三棱锥的体积为( )| A. | $\frac{{\sqrt{2}}}{12}$ | B. | $\frac{{\sqrt{3}}}{12}$ | C. | $\frac{1}{8}$ | D. | $\frac{{\sqrt{3}}}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
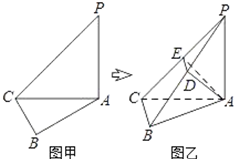 如图甲,在平面四边形PABC中,PA=AC=2,PA=AC=2,∠P=45°,∠B=90°,∠PCB=105°,现将四边形PABC沿AC折起,使平面PAC⊥平面ABC(如图乙),点D是棱PB的中点.
如图甲,在平面四边形PABC中,PA=AC=2,PA=AC=2,∠P=45°,∠B=90°,∠PCB=105°,现将四边形PABC沿AC折起,使平面PAC⊥平面ABC(如图乙),点D是棱PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 92012 | B. | 272012 | C. | 92013 | D. | 272013 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com