
分析 (1)利用二倍角余弦公式的变形、两角差的正弦公式化简解析式,由三角函数的周期公式函数f(x)的最小正周期,由正弦函数的单调区间求出f(x)的递增区间;
(2)由(1)化简f(θ)=$\frac{5}{6}$,由θ的范围求出2θ-$\frac{π}{6}$的范围,由平方关系求出$cos(2θ+\frac{π}{6})$ 的值,由两角差的正弦公式求出sin2θ的值.
解答 解:(1)由题意得,f(x)=cos2x-$\sqrt{3}$sinxcosx+1
=$\frac{1}{2}$(1+cos2x)-$\frac{\sqrt{3}}{2}$sin2x+1=$-sin(2x-\frac{π}{6})+\frac{3}{2}$,
∴函数f(x)的最小正周期T=$\frac{2π}{2}=π$,
由$\frac{π}{2}+2kπ≤2x-\frac{π}{6}≤\frac{3π}{2}+2kπ(k∈Z)$得,
$\frac{π}{3}+kπ≤x≤\frac{5π}{6}+kπ(k∈Z)$,
∴f(x)的单调递增区间是$[\frac{π}{3}+kπ,\frac{5π}{6}+kπ](k∈Z)$;
(2)由(1)得,f(θ)=$-sin(2θ-\frac{π}{6})+\frac{3}{2}$=$\frac{5}{6}$,
化简得,$sin(2θ-\frac{π}{6})=\frac{2}{3}$>0,
由$\frac{π}{3}$<θ<$\frac{2π}{3}$得,$\frac{π}{2}$<2θ-$\frac{π}{6}$<$\frac{7π}{6}$,
∴$cos(2θ+\frac{π}{6})$=$-\sqrt{1-si{n}^{2}(2θ+\frac{π}{6})}$=$-\frac{\sqrt{5}}{3}$,
∴sin2θ=sin[(2θ+$\frac{π}{6}$)-$\frac{π}{6}$]=sin$(2θ+\frac{π}{6})$ cos$\frac{π}{6}$-cos $(2θ+\frac{π}{6})$ sin$\frac{π}{6}$
=$\frac{2}{3}×\frac{\sqrt{3}}{2}-(-\frac{\sqrt{5}}{3})×\frac{1}{2}$=$\frac{2\sqrt{3}+\sqrt{5}}{6}$.
点评 本题考查正弦函数的图象与性质,三角恒等变换中的公式在化简、求值中的应用,注意角的范围和三角函数值的符号,考查化简变形、计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | a1+a101>0 | B. | a2+a100<0 | C. | a3+a100≤0 | D. | a51=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
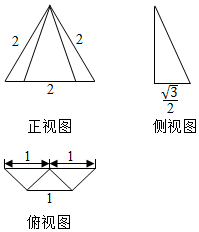
| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{6}}{4}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
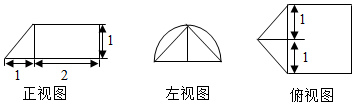 某几何体的三视图如图所示,若该几何体的体积为$\frac{1}{3}$+π,则a=( )
某几何体的三视图如图所示,若该几何体的体积为$\frac{1}{3}$+π,则a=( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
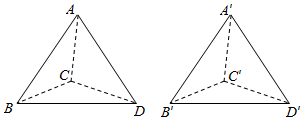 如图将棱长为2的正四面体ABCD水平平移3个单位后得到A′B′C′D′,则在这个平移过程中直线CD′与BA′之间的距离为d.则( )
如图将棱长为2的正四面体ABCD水平平移3个单位后得到A′B′C′D′,则在这个平移过程中直线CD′与BA′之间的距离为d.则( )| A. | d=2 | B. | d=$\sqrt{2}$ | C. | d∈[$\sqrt{2}$,2] | D. | d∈[1,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
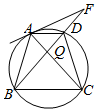 如图所示,四边形ABCD中,AD∥BC,AB=CD,AC,BD交于点Q,∠BAC=∠CAD,AP为四边形ABCD外接圆的切线,交BD的延长线于点P.
如图所示,四边形ABCD中,AD∥BC,AB=CD,AC,BD交于点Q,∠BAC=∠CAD,AP为四边形ABCD外接圆的切线,交BD的延长线于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
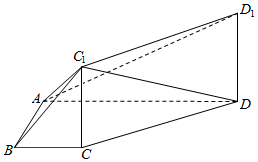 如图,四边形ABCD是梯形,AD∥BC,∠BAD=90°,DD1⊥面ABCD,DD1∥CC1,AD=4,AB=2,BC=1.
如图,四边形ABCD是梯形,AD∥BC,∠BAD=90°,DD1⊥面ABCD,DD1∥CC1,AD=4,AB=2,BC=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com