练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知数列{an}，{bn}满足a1=b1=3，an+1-an=$\frac{{{b_{n+1}}}}{b_n}$=3，n∈N*，若数列{cn}满足cn=b1an，则c2013=（　　）
    A．92012B．272012C．92013D．272013

    分析 利用等差数列与等比数列的通项公式即可得出．

    解答 解：∵数列{an}，{bn}满足a1=b1=3，an+1-an=$\frac{{{b_{n+1}}}}{b_n}$=3，
    ∴数列{an}，{bn}分别是等差数列与等比数列，
    ∴an=3+3（n-1）=3n，bn=3n，cn=b1an=33n．
    ∴c2013=33×2013=272013，
    故选：D．

    点评 本题考查了等差数列与等比数列的通项公式，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

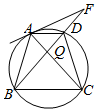    17．如图所示，四边形ABCD中，AD∥BC，AB=CD，AC，BD交于点Q，∠BAC=∠CAD，AP为四边形ABCD外接圆的切线，交BD的延长线于点P．
    （1）求证：PQ2=PD•PB；
    （2）若AB=3，AP=2，AD=$\frac{4}{3}$，求AQ的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．给出下列几个式子：
    （1）tan25°+tan35°+$\sqrt{3}$tan25°tan35°；   
    （2）$\frac{1+tan15°}{1-tan15°}$；
    （3）2（sin35°cos25°+sin55°cos65°）；     
    （4）$\frac{2tan\frac{π}{6}}{1-ta{n}^{2}\frac{π}{6}}$．
    其中结果为$\sqrt{3}$的式子的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．等差数列{an}的前n项和Sn，若a3=7，S7=35，则a8=（　　）
    A．-3B．-4C．-5D．-6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

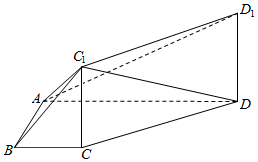    2．如图，四边形ABCD是梯形，AD∥BC，∠BAD=90°，DD1⊥面ABCD，DD1∥CC1，AD=4，AB=2，BC=1．
    （Ⅰ）求证：BC1∥平面ADD1；
    （Ⅱ）若DD1=2，求平面AC1D1与平面ADD1所成的锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．二项式（ax+$\frac{{\sqrt{3}}}{6}$）6的展开式中x5的系数为$\sqrt{3}$，则$\int_0^a$x2dx=（　　）
    A．$\frac{1}{3}$B．$\frac{1}{2}$C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．某初级中学有学生270人，其中一年级108人，二、三年级各81人，现要利用抽样方法抽取10人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样时，将学生按一、二、三年级依次统一编号为1，2，…，270；使用系统抽样时，将学生统一随机编号1，2，…，270，并将整个编号依次分为10段．如果抽得号码有下列四种情况：
    ①7，34，61，88，115，142，169，196，223，250；
    ②5，9，100，107，111，121，180，195，200，265；
    ③11，38，65，92，119，146，173，200，227，254；
    ④30，57，84，111，138，165，192，219，246，270；
    关于上述样本的下列结论中，正确的是（　　）
    A．②、③都不能为系统抽样B．②、④都不能为分层抽样
    C．①、④都可能为系统抽样D．①、③都可能为分层抽样

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

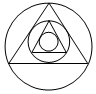    16．记半径为1的圆为C1，C1的外切正三角形的外接圆为C2，C2的外切正三角形的外接圆C3，…Cn-1的外切正三角形的外接圆为Cn，则C16的面积是（　　）
    A．215•πB．216•πC．230•πD．232•π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知f（x） 是定义在R上且以2为周期的偶函数，当0≤x≤1时，f（x）=x2，如果直线y=x+a与曲线y=f（x） 恰有三个不同的交点，则实数a的取值范围是（　　）
    A．[2k，2k+$\frac{1}{4}$]（k∈Z）B．（2k-$\frac{1}{4}$，2k）（k∈Z）C．（2k-$\frac{1}{2}$，2k）（k∈Z）D．（2k，2k+$\frac{1}{4}$）（k∈Z）

    查看答案和解析>>

    同步练习册答案