
| A. | ②、③都不能为系统抽样 | B. | ②、④都不能为分层抽样 | ||
| C. | ①、④都可能为系统抽样 | D. | ①、③都可能为分层抽样 |
科目:高中数学 来源: 题型:解答题
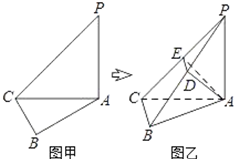 如图甲,在平面四边形PABC中,PA=AC=2,PA=AC=2,∠P=45°,∠B=90°,∠PCB=105°,现将四边形PABC沿AC折起,使平面PAC⊥平面ABC(如图乙),点D是棱PB的中点.
如图甲,在平面四边形PABC中,PA=AC=2,PA=AC=2,∠P=45°,∠B=90°,∠PCB=105°,现将四边形PABC沿AC折起,使平面PAC⊥平面ABC(如图乙),点D是棱PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 92012 | B. | 272012 | C. | 92013 | D. | 272013 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{6}{π}$ | C. | $\frac{3}{2π}$ | D. | $\root{3}{\frac{6}{π}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P1,P2 | B. | P1,P4 | C. | P2,P3 | D. | P3,P4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,5) | B. | [-4,5) | C. | {-4,-3,0} | D. | {0,1,2,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com