
分析 (Ⅰ)由g(x)≤0得42x-5•22x+1+16≤0,然后利用换元法解一元二次不等式即可得答案;
(Ⅱ)化简函数f(x),然后利用换元法求解即可得答案.
解答 解:(Ⅰ)由集合A={x|g(x)≤0},
得g(x)≤0即42x-5•22x+1+16≤0,
则42x-10•4x+16≤0,
令t=4x,即有t2-10t+16≤0,
得(t-2)(t-8)≤0,即2≤t≤8,2≤4x≤8,${4^{\frac{1}{2}}}≤{4^x}≤{4^{\frac{3}{2}}}$,
解得$A=\{x|\frac{1}{2}≤x≤\frac{3}{2}\}$;
(Ⅱ)$f(x)=({log_2}-{log_2}4)({log_4}4-{log_4}{x^2})=({log_2}x-2)({log_2}x+1)$,
令$u={log_2}x∈[-1,{log_2}\frac{3}{2}]$
则$y={u^2}-u-2,u∈[-1,{log_2}\frac{3}{2}]$,
二次函数的对称轴${u_0}=\frac{1}{2}∈[-1,{log_2}\frac{3}{2}]$,
∴$y∈[-\frac{9}{4},0]$.
点评 本题考查了指、对数不等式的解法,考查了会用换元法解决问题,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
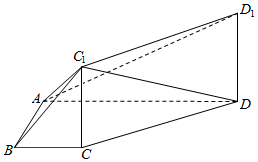 如图,四边形ABCD是梯形,AD∥BC,∠BAD=90°,DD1⊥面ABCD,DD1∥CC1,AD=4,AB=2,BC=1.
如图,四边形ABCD是梯形,AD∥BC,∠BAD=90°,DD1⊥面ABCD,DD1∥CC1,AD=4,AB=2,BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②、③都不能为系统抽样 | B. | ②、④都不能为分层抽样 | ||
| C. | ①、④都可能为系统抽样 | D. | ①、③都可能为分层抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有一个解 | B. | 有两个解 | C. | 不能确定 | D. | 无解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com