
分析 将根式化为分数指数幂的形式,然后利用幂的运算法则化简代数式
解答 解:(1)$\sqrt{a}$=${a}^{\frac{1}{2}}$,(a>0);
(2)$\root{3}{{x}^{2}}$=${x}^{\frac{2}{3}}$;
(3)$\frac{1}{\root{3}{a}}$=${a}^{-\frac{1}{3}}$;
(4)$\sqrt{{x}^{3}}$=${x}^{\frac{3}{2}}$(x>0);
(5)$\sqrt{{x}^{4}{y}^{3}}$=${x}^{2}{y}^{\frac{3}{2}}$(y>0);
(6)$\frac{{m}^{2}}{\sqrt{m}}$=${m}^{\frac{3}{2}}$(m>0);
(7)$\root{3}{(a+b)^{2}}$=$(a+b)^{\frac{2}{3}}$;
(8)$\sqrt{(m-n)^{2}}$=m-n,(m>n)
点评 本题考查分数指数幂与根式之间的转化,在解决根式的化简时应该先将根式化为分数指数幂,然后利用幂的运算法则进行计算,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $({-∞,\frac{19}{6}})$ | B. | $({-∞,\frac{3}{2}})$ | C. | $({-∞,\frac{9}{4}})$ | D. | (-∞,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 6 | C. | -2或6 | D. | 2或6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
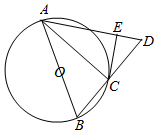 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com