分析:(Ⅰ)连接A1B交AB1于G点,连接MG,根据四边形ABB1A1为平行四边形得到A1G=BG,又因A1M=C1M,则MG∥BC1,又MG?平面AMB1,BC1?平面AMB1
根据线面平行的判定定理可知BC1∥平面AMB1.
(Ⅱ)平面ABC∥平面A1B1C1,平面MB1A与平面ABC所成的二面角等于平面MB1A与平面平面A1B1C1所成的二面角.∠A1MA为平面MB1A与平面平面A1B1C1,所成的二面角的平面角
(Ⅲ)转化V B-AMB1=V M-BAB1,利用体积公式计算.
解答:证明:(Ⅰ)连接A
1B交AB
1于G点,连接MG
∵四边形ABB
1A
1为平行四边形∴A
1G=MG
又∵A
1M=C
1M∴MG∥BC
1又∵MG?平面AMB
1BC
1?平面AMB
1∴BC
1∥平面AMB
1(Ⅱ)平面ABC∥平面A
1B
1C
1,平面MB
1A与平面ABC所成的二面角等于平面MB
1A与平面平面A
1B
1C
1所成的二面角.
面MB
1A∩面A
1B
1C
1=MB
1,
由已知,AA
1⊥平面A
1B
1C
1,AA
1⊥MB
1,又A
1M⊥MB
1,∴∠A
1MA为平面MB
1A与平面平面A
1B
1C
1,所成的二面角的平面角.
在RT△A
1MA中,tan∠A
1MA=
=2(Ⅲ)V
B-AMB1=V
M-BAB1,
S
△ABB1=
a2,M到面BAB
1的距离等于C
1到面BAB
1的距离的一般,h=
×a=a,
所以V
B-AMB1=V
M-BAB1=
×a2×a= 点评:本题考查空间直线和平面平行,空间角、体积的计算.考查空间想象、转化、推理论证能力.

 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1的中点
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1的中点

 阅读快车系列答案
阅读快车系列答案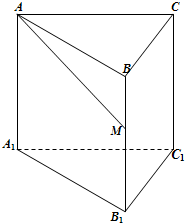 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ. 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.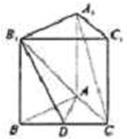 如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1. (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.