Question

关于x的不等式x²+9+|x²-3x|≥kx在x∈[1，5]上恒成立，则实数k的取值范围是

1. A.
   （-∞，6]
2. B.
   （-∞，6）
3. C.
   （0，6]
4. D.
   [6，+∞）

Answer 1

A
分析：令f（x）=x²+9+|x²-3x|，x∈[1，5]，由已知，k只需小于或等于g（x）=的最小值即可．写出分段函数g（x）的函数解析式，求出其最小值即可解决．
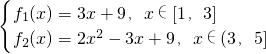
解答：令f（x）=x²+9+|x²-3x|，x∈[1，5]，则f（x）=，由已知，k只需小于或等于g（x）=的最小值即可．
当x∈[1，3]时，g（x）==3+≥6，
当x∈（3，5]时，g（x）==2x+-3，g′（x）=（）′=2-＞0，是增函数，g（x）＞g（3）=6，
所以g（x）的最小值为6，所以k≤6．
故选A
点评：本题考查不等式恒成立问题，考查分段函数的性质、参数分离的方法．