
����Ŀ��һ�죬���ó�һ��װ�����ſ�Ƭ�ĺ��ӣ�һ�ſ�Ƭ�����涼����ɫ��һ�ſ�Ƭ�����涼����ɫ������һ�ſ�Ƭһ������ɫ����һ������ɫ��������˵��һ����Ϸ�������ǣ���������Ŀ�Ƭ˳����Һ�����������һ�ſ�Ƭ���������ϣ�Ȼ��Ƭ���µ������ɫ����ʤ����������µ������ɫ�볯�ϵ������ɫһ�£����Ӯ���������.�Ҷ���Ϸ�Ĺ�ƽ����������ɣ����Ǽ�˵������Ȼ��ƽ���㿴��������ϵ������ɫΪ��ɫ�������ſ�Ƭ���������涼����ɫ����˳��µ���Ҫô����ɫ��Ҫô����ɫ����ˣ���Ӯ�ĸ���Ϊ![]() ����Ӯ�ĸ���Ҳ��
����Ӯ�ĸ���Ҳ��![]() ����ô����ƽ�������������Ϸ�Ƿ�ƽ.
����ô����ƽ�������������Ϸ�Ƿ�ƽ.
���𰸡�������.
��������
�ѿ�Ƭ���������ɫ��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����У�G��ʾ��ɫ��B��ʾ��ɫ��
�����У�G��ʾ��ɫ��B��ʾ��ɫ��![]() ��
��![]() ��������ɫ��һ�������ſ�Ƭ����ɫ��������ͼ�õ������ռ䣬��������ʼ����ж�.
��������ɫ��һ�������ſ�Ƭ����ɫ��������ͼ�õ������ռ䣬��������ʼ����ж�.
�⣺�ѿ�Ƭ���������ɫ��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���У�G��ʾ��ɫ��B��ʾ��ɫ��![]() ��
��![]() ��������ɫ��һ�������ſ�Ƭ����ɫ.
��������ɫ��һ�������ſ�Ƭ����ɫ.
��Ϸ���еĽ����������ͼ��ʾ.

���ѿ�������ʱ�������ռ��й���6�������㣬���ϵ����볯�µ�����ɫ��һ�µ����ֻ��2�֣������Ӯ�ĸ���Ϊ![]() .
.
��ˣ������Ϸ����ƽ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����a>b>0���ԱȽ�![]() ��
��![]() �Ĵ�С��
�Ĵ�С��
��2��������x�IJ���ʽ(2x��1)2<ax2�Ľ⼯������ǡ����3������ʵ��a��ȡֵ��Χ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��С�ס�����λͬѧ�����Ҳ��Ż�ץ��ÿ������ץ1�������ץ3���涨˭ץ�����һ����Ӯ.�������ץ����ô�����ƶ���ȷ����_____________.(��д���)
��С�ס�����λͬѧ�����Ҳ��Ż�ץ��ÿ������ץ1�������ץ3���涨˭ץ�����һ����Ӯ.�������ץ����ô�����ƶ���ȷ����_____________.(��д���)
����![]() ������б�Ӯ�IJ��ԣ� ����
������б�Ӯ�IJ��ԣ� ����![]() �������б�Ӯ�IJ��ԣ�
�������б�Ӯ�IJ��ԣ�
����![]() ������б�Ӯ�IJ��ԣ� ����
������б�Ӯ�IJ��ԣ� ����![]() �������б�Ӯ�IJ���.
�������б�Ӯ�IJ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������dz�������ϵͳ��һ�ִ���ģʽ�����ڽ�����ڳ��С����һ����������ر��Ч������ͣȡ���㡢���ü۸��������ɫ���������ܵ����ǵ�������ij���г���Ϊ����������˾��������ʽ�ĵ�������֪��������ʽ�����Ĺ̶��ɱ�Ϊ20 000Ԫ��ÿ����һ������ʽ������Ҫ����Ͷ��100Ԫ�����ݳ������㣬���г�����������(��λ��Ԫ)����ֶκ���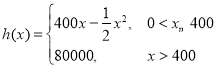 ����x������ʽ�������²���(��λ����)�����������棭�ܳɱ���
����x������ʽ�������²���(��λ����)�����������棭�ܳɱ���
(1)�Խ����г���������yԪ��ʾΪ�²���x�ĺ�����
(2)���²���Ϊ���ټ�ʱ���г��������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���չ�˾����ÿ�¸�����Աȷ�������������Ŀ�꣬������Աʵ��Ŀ�����.����Ŀ��ȷ�����ʵ����ֱ��Ӱ�칫˾�ľ���Ч�������Ա�Ĺ��������ԣ�Ϊ�ˣ��ù�˾���������ȡ��50λ����Ա�ϸ��µ������۶��λ����Ԫ�������Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.

��1���ٸ���ͼ�����ݣ���������۶���![]() С���ڵ�Ƶ��.
С���ڵ�Ƶ��.
�ڸ���ֱ��ͼ���ƣ�������Ŀ�궨Ϊ������Ԫʱ���ܹ�ʹ70%������Ա�������˵������.
��2���ù�˾�����������۶�Ϊ![]() ��
��![]() ������С���У�ѡȡ2λ����Ա�������۾��飬��ѡ��������Ա����ͬһ��С��ĸ���.
������С���У�ѡȡ2λ����Ա�������۾��飬��ѡ��������Ա����ͬһ��С��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г����飬ij���в���һ��С��Ʒ�ڹ�ȥ��20���ڵ�����������������۸���Ԫ����Ϊʱ��![]() �������ĺ����������������������㺯��
�������ĺ����������������������㺯��![]() ���������������ۼ۸����������
���������������ۼ۸���������� ��Ԫ����
��Ԫ����
��1����д��������Ʒ�������۶�![]() ��ʱ��
��ʱ��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2���������Ʒ�������۶�![]() �����ֵ����Сֵ��
�����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ˮ������ÿ����![]() Ԫ/ǧ�˵ļ۸��ˮ�����ع�������
Ԫ/ǧ�˵ļ۸��ˮ�����ع�������![]() ˮ����Ȼ����
ˮ����Ȼ����![]() Ԫ/ǧ�˵ļ۸���ۣ�����ʣ�࣬��ʣ�µ�ˮ����
Ԫ/ǧ�˵ļ۸���ۣ�����ʣ�࣬��ʣ�µ�ˮ����![]() Ԫ/ǧ�˵ļ۸��˻�ˮ�����أ�Ϊ��ȷ�������������ó��м�¼��
Ԫ/ǧ�˵ļ۸��˻�ˮ�����أ�Ϊ��ȷ�������������ó��м�¼��![]() ˮ�����
ˮ�����![]() ���������������λ��ǧ�ˣ����������±���
���������������λ��ǧ�ˣ����������±���
�������� |
|
|
|
|
|
|
|
Ƶ�� |
|
|
|
|
|
|
|
��![]() ���¼�ĸ�����������Ƶ�ʴ�������������ĸ���.
���¼�ĸ�����������Ƶ�ʴ�������������ĸ���.
��1����ó���![]() ˮ����������
ˮ����������![]() ����λ��ǧ�ˣ��ķֲ��У�
����λ��ǧ�ˣ��ķֲ��У�
��2�����ó���һ�칺��![]() ˮ��
ˮ��![]() ǧ�ˣ��dz��е���
ǧ�ˣ��dz��е���![]() ˮ����õ�����Ϊ
ˮ����õ�����Ϊ![]() ����λ��Ԫ������
����λ��Ԫ������![]() �ķֲ��м�����ѧ����.
�ķֲ��м�����ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��ԲC��![]() ��a��b��0���Ľ���Ϊ2��
��a��b��0���Ľ���Ϊ2��
��1������ԲC�����㣨![]() ��1��������ԲC�ı����̣�
��1��������ԲC�ı����̣�
��2����A����2��0����FΪ��ԲC���㣬����ԲC�ϴ��ڵ�P������![]() ������ԲC�������ʵ�ȡֵ��Χ��
������ԲC�������ʵ�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����б������![]() �У�
�У�![]() ��ƽ��
��ƽ��![]() ����
����![]() ����
����![]() ��D�ֱ����߶�
��D�ֱ����߶�![]() ��BC���е㣮
��BC���е㣮

��1����֤��![]() ��
��
��2����֤��AD//ƽ��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com