
设数列 满足
满足 ,
, .
.
(1)求 ;
;
(2)先猜想出 的一个通项公式,再用数学归纳法证明你的猜想.
的一个通项公式,再用数学归纳法证明你的猜想.
(1)5,7,9;(2)猜想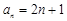 ;证明祥见解析.
;证明祥见解析.
解析试题分析:(1)由已知等式: 令n=1,再将
令n=1,再将 代入即可求得
代入即可求得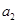 的值;再令n=2并将
的值;再令n=2并将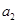 的值就可求得
的值就可求得 的值;最后再令n=2并将
的值;最后再令n=2并将 的值就可求得
的值就可求得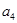 的值;(2)由已知及(1)的结果,可猜想出
的值;(2)由已知及(1)的结果,可猜想出 的一个通项公式;用数学归纳法证明时应注意格式:①验证
的一个通项公式;用数学归纳法证明时应注意格式:①验证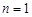 时猜想正确;②作归纳假设:假设当
时猜想正确;②作归纳假设:假设当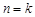 时,猜想成立,在此基础上来证明
时,猜想成立,在此基础上来证明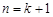 时猜想也成立,注意在此证明过程中要充分利用已知条件找出
时猜想也成立,注意在此证明过程中要充分利用已知条件找出 之间的关系,并一定要用到假设当
之间的关系,并一定要用到假设当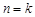 时的结论;最后一定要下结论.
时的结论;最后一定要下结论.
试题解析: (1)由条件 ,依次得
,依次得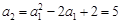 ,
,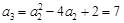 ,
,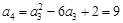 , 6分
, 6分
(2)由(1),猜想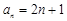 . 7分
. 7分
下用数学归纳法证明之:
①当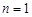 时,
时,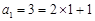 ,猜想成立; 8分
,猜想成立; 8分
②假设当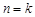 时,猜想成立,即有
时,猜想成立,即有 , 9分
, 9分
则当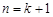 时,有
时,有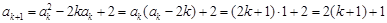 ,
,
即当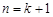 时猜想也成立, 13分
时猜想也成立, 13分
综合①②知,数列 通项公式为
通项公式为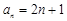 . 14分
. 14分
考点:1.数列的概念;2.归纳猜想;3.数学归纳法.


科目:高中数学 来源: 题型:填空题
如图所示的数阵叫“莱布尼兹调和三角形”,他们是由正整数的倒数组成的,第 行有
行有 个数且两端的数均为
个数且两端的数均为 ,每个数是它下一行左右相邻两数的和,如:
,每个数是它下一行左右相邻两数的和,如: …,则第
…,则第 行第3个数字是
行第3个数字是 .(用含
.(用含 的式子作答)
的式子作答)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
① 是数列
是数列 的前
的前 项和,若
项和,若 ,则数列
,则数列 是等差数列
是等差数列
②若 ,则
,则
③已知函数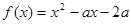 ,若存在
,若存在 ,使得
,使得 成立,则
成立,则
④在 中,
中, 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 则
则 为等腰直角三角形
为等腰直角三角形
其中正确的有 (填上所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知4个命题:
①若等差数列 的前n项和为
的前n项和为 则三点
则三点 共线;
共线;
②命题:“ ”的否定是“
”的否定是“ ”;
”;
③若函数 在(0,1)没有零点,则k的取值范围是
在(0,1)没有零点,则k的取值范围是
④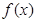 是定义在R上的奇函数,
是定义在R上的奇函数, 的解集为(
的解集为( 2,2)
2,2)
其中正确的是 。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高一学生1000人,每周一次同时在两个可容纳600人的会议室,开设“音乐欣赏”与“美术鉴赏”的校本课程.要求每个学生都参加,要求第一次听“音乐欣赏”课的人数为
 ,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用
,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用 分别表示在第
分别表示在第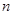 次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
(1)若 ,分别求出第二次,第三次选“音乐欣赏”课的人数
,分别求出第二次,第三次选“音乐欣赏”课的人数 ;
;
(2)①证明数列 是等比数列,并用
是等比数列,并用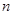 表示
表示 ;
;
②若要求前十次参加“音乐欣赏”课的学生的总人次不超过5800,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com