【题目】在平面直角坐标系
中，点
，若在曲线
上存在点
使得
，则实数
的取值范围为__________
【答案】
【解析】
根据题意，设P（x，y），分析可得若|PB|＝2|PA|，则有（x﹣4）2+y2＝4（x﹣1）2+4y2，变形可得x2+y2＝4，进而可得P的轨迹为以O为圆心，半径为2的圆；将曲线C的方程变形为（x﹣a）2+（y﹣2a）2＝9，可得以（a，2a）为圆心，半径为3的圆；据此分析可得若曲线C上存在点P使得|PB|＝2|PA|，则圆C与圆x2+y2＝4有公共点，由圆与圆的位置关系可得3﹣2
2+3，解可得a的取值范围，即可得答案．
根据题意，设P（x，y），
若|PB|＝2|PA|，即|PB|2＝4|PA|2，则有（x﹣4）2+y2＝4（x﹣1）2+4y2，
变形可得：x2+y2＝4，
即P的轨迹为以O为圆心，半径为2的圆，
曲线Cx2﹣2ax+y2﹣4ay+5a2﹣9＝0，即（x﹣a）2+（y﹣2a）2＝9，则曲线C是以（a，2a）为圆心，半径为3的圆；
若曲线C上存在点P使得|PB|＝2|PA|，则圆C与圆x2+y2＝4有公共点，
则有3﹣22+3，即1
|a|≤5，
解可得：
a
或
a，
即a的取值范围为：[
，
]∪[
，
]；
故答案为：[，]∪[，]．
阅读快车系列答案科目：高中数学 来源： 题型：
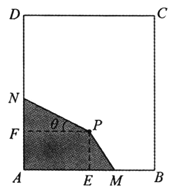
【题目】（题文）如图，长方形材料
中，已知
，
.点
为材料内部一点，
于
，
于
，且
，
. 现要在长方形材料中裁剪出四边形材料
，满足
，点
、
分别在边
，
上.
（1）设
，试将四边形材料的面积表示为
的函数，并指明的取值范围；
（2）试确定点在上的位置，使得四边形材料的面积
最小，并求出其最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2017年“双节”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速
分成六段： 
， 
， 
， 
， 
， 
后得到如图的频率分布直方图．
（1）调查公司在采样中，用到的是什么抽样方法？
（2）求这40辆小型车辆车速的众数、中位数及平均数的估计值；
（3）若从车速在
的车辆中任抽取2辆，求车速在的车辆至少有一辆的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
是不重合直线，
是不重合平面，则下列命题
①若
，则
∥
②若
∥
∥，则∥
③若∥、
∥，则∥
④若
，则
∥
⑤若
，则∥
为假命题的是
A. ①②③ B. ①②⑤ C. ③④⑤ D. ①②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，平面中两条直线
和
相交于点O，对于平面上任意一点M，若p，q分别是M到直线和的距离，则称有序非负实数对
是点M的“距离坐标”.下列四个命题中正确命题为( )
A.若
，则“距离坐标”为
的点有且仅有1个
B.若
，且
，则“距离坐标”为的点有且仅有2个
C.若
，则“距离坐标”为的点有且仅有4个
D.若
，则点M在一条过点O的直线上
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱ABC-A1B1C1中，△ABC和△AA1C均是边长为2的等边三角形，点O为AC中点，平面AA1C1C⊥平面ABC．
（1）证明：A1O⊥平面ABC；
（2）求直线AB与平面A1BC1所成角的正弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
