练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知α为第二象限角．且sin2α=-$\frac{24}{25}$，则cosα-sinα的值为（　　）
    A．$\frac{7}{5}$B．-$\frac{7}{5}$C．$\frac{1}{5}$D．-$\frac{1}{5}$

    分析 由α的范围和三角函数值的符号判断出cosα-sinα的符号，由条件、平方关系、二倍角的正弦函数求出cosα-sinα的值．

    解答 解：∵α为第二象限角，∴cosα-sinα＜0，
    ∵sin2α=-$\frac{24}{25}$，
    ∴cosα-sinα=-$\sqrt{（cosα-sinα）^{2}}$=$-\sqrt{1-sin2α}$
    =$-\sqrt{1+\frac{24}{25}}$=$-\frac{7}{5}$，
    故选B．

    点评 本题考查二倍角的正弦函数，平方关系，以及三角函数值的符号，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    16．若${∫}_{1}^{t}$（-$\frac{1}{x}$+2x）dx=3-ln2，则t=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

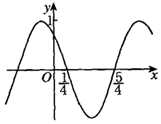    17．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，则下列说法错误的是（　　）
    A．ω=π
    B．φ=$\frac{π}{4}$
    C．f（x）的单调减区间为（2k-$\frac{1}{4}$，2k+$\frac{3}{4}$），k∈Z
    D．f（x）的对称中心是（k+$\frac{1}{4}$，0），k∈Z

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．传承传统文化再掀热潮，央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏．将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级，随机从中抽取了100名选手进行调查，下面是根据调查结果绘制的选手等级人数的条形图．
    （Ⅰ）若将一般等级和良好等级合称为合格等级，根据已知条件完成下面的2×2列联表，并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关？
    优秀合格合计
    大学组
    中学组
    合计
    注：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
    P（k2≥k0）0.100.050.005
    k02.7063.8417.879
    （Ⅱ）若参赛选手共6万人，用频率估计概率，试估计其中优秀等级的选手人数；
    （Ⅲ）在优秀等级的选手中取6名，依次编号为1，2，3，4，5，6，在良好等级的选手中取6名，依次编号为1，2，3，4，5，6，在选出的6名优秀等级的选手中任取一名，记其编号为a，在选出的6名良好等级的选手中任取一名，记其编号为b，求使得方程组$\left\{\begin{array}{l}ax+by=3\\ x+2y=2\end{array}\right.$有唯一一组实数解（x，y）的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知等差数列{an}中，公差d≠0，a4=10，且a3，a6，a10成等比数列，则数列{an}前9项的和为（　　）
    A．99B．90C．84D．70

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．甲乙丙三人代表班级参加校运会的跑步，跳远，铅球比赛，每人参加一项，每项都要有人参加，他们的身高各不同，现了解到已下情况：
    （1）甲不是最高的；（2）最高的是没报铅球；（3）最矮的参加了跳远；（4）乙不是最矮的，也没参加跑步．
    可以判断丙参加的比赛项目是跑步．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若无论实数a取何值时，直线ax+y+a+1=0与圆x2+y2-2x-2y+b=0都相交，则实数b的取值范围．（　　）
    A．（-∞，2）B．（2，+∞）C．（-∞，-6）D．（-6，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知平面向量$\overrightarrow a，\overrightarrow b$满足$\overrightarrow b•（\overrightarrow a+\overrightarrow b）=3$，且$|\overrightarrow a|=1，|\overrightarrow b|=2$，则向量$\overrightarrow a$与$\overrightarrow b$的夹角（　　）
    A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=x-a-lnx（a∈R）．
    （1）若f（x）≥0恒成立，求实数a的取值范围；
    （2）证明：若0＜x1＜x2，则x1lnx1-x1lnx2＞x1-x2．

    查看答案和解析>>

    同步练习册答案