练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知集合A=（2，4），B=（a，3a）
    （1）若AB，求实数a的取值范围；
    （2）若A∩B≠，求实数a的取值范围．

    【答案】解：集合A=（2，4），B=（a，3a）；
    （1）当AB时，应满足，
    解得≤a≤2，
    所以实数a的取值范围是≤a≤2；
    （2）当A∩B≠时，应满足2＜a＜4或2＜3a＜4，
    解得2＜a＜4或＜a＜，
    即＜a＜4；
    所以实数a的取值范围是＜a＜4．
    【解析】（1）根据AB时，满足 ， 求出a的取值范围；
    （2）根据A∩B≠时，满足2＜a＜4或2＜3a＜4，求出a的取值范围．
    【考点精析】认真审题，首先需要了解集合的交集运算(交集的性质：（1）A∩BA，A∩BB，A∩A=A，A∩=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A，B两种不同的教学方式分别在甲、乙两个班进行教改实验．为了了解教学效果，期末考试后，陈老师对甲、乙两个班级的学生成绩进行统计分析，画出频率分布直方图(如下图)．记成绩不低于90分者为“成绩优秀”．

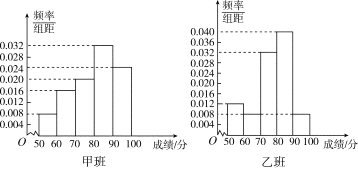
    （Ⅰ）根据频率分布直方图填写下面2×2列联表；

    甲班(A方式)

    乙班(B方式)

    总计

    成绩优秀

    成绩不优秀

    总计

    （Ⅱ）判断能否在犯错误的概率不超过0.05的前提下认为：“成绩优秀”与教学方式有关？

    附：.

    P(K2≥k)

    0.25

    0.15

    0.10

    0.05

    0.025

    k

    1.323

    2.072

    2.706

    3.841

    5.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（， ），曲线在处的切线方程为.

    （Ⅰ）求， 的值；

    （Ⅱ）证明： ；

    （Ⅲ）已知满足的常数为.令函数（其中是自然对数的底数， ），若是的极值点，且恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数的单调区间与极值；

    （2）当时，令，若在上有两个零点，求实数的取值范围；

    （3）当时，函数的图像上所有点都在不等式组所表示的平面区域内，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在研究塞卡病毒（Zika virus）某种疫苗的过程中，为了研究小白鼠连续接种该种疫苗后出现症状的情况，做接种试验，试验设计每天接种一次，连续接种3天为一个接种周期．已知小白鼠接种后当天出现症状的概率为，假设每次接种后当天是否出现症状与上次接种无关．

    （1）若出现症状即停止试验，求试验至多持续一个接种周期的概率；

    （2）若在一个接种周期内出现3次 症状，则这个接种周期结束后终止试验，试验至多持续3个周期，设接种试验持续的接种周期数为 ，求 的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商品在近30天内每件的销售价格P（元）与时间t（天）的函数是：P=
    该商品的日销售量Q（件）与时间t（天）的函数关系是：Q=﹣t+40（0＜t≤30，t∈N*），求这种商品的日销售金额的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）若，试讨论函数的单调性；

    （Ⅱ）设，当对任意的恒成立时，求函数的最大值的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知一个几何体的三视图如下图，大致画出它的直观图，并求出它的表面积和体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求满足下列条件的直线方程：
    （1）求经过直线l1：x+3y﹣3=0，l2：x﹣y+1=0的交点，且平行于直线2x+y﹣3=0的直线l方程；
    （2）求在两坐标轴上截距相等，且与点A（3，1）的距离为的直线l的方程．

    查看答案和解析>>

    同步练习册答案