
分析 (1)由Tn=-an+$\frac{1}{2},n∈{N^*}$,可得n=1时,a1=-a1+$\frac{1}{2}$,解得a1.n≥2时,an=Tn-Tn-1,化为:an=$\frac{1}{2}{a}_{n-1}$,利用等比数列的通项公式即可得出,所以bn+2=3$lo{g}_{\frac{1}{2}}$$(\frac{1}{2})^{n+1}$,可得bn.
(2)由(1)知,cn=an•bn=(3n+1)$•(\frac{1}{2})^{n+1}$.利用错位相减法即可得出.
(3)利用数列的单调性、不等式的解法即可得出.
解答 解:(1)由Tn=-an+$\frac{1}{2},n∈{N^*}$,∴n=1时,a1=-a1+$\frac{1}{2}$,解得a1=$\frac{1}{4}$.
n≥2时,an=Tn-Tn-1=-an+$\frac{1}{2}$-$(-{a}_{n-1}+\frac{1}{2})$,化为:an=$\frac{1}{2}{a}_{n-1}$,
∴数列{an}是公比为$\frac{1}{2}$的等比数列,
则an=$(\frac{1}{2})^{n+1}$(n∈N?),…(2分)
所以bn+2=3$lo{g}_{\frac{1}{2}}$$(\frac{1}{2})^{n+1}$=3n+3,即bn=3n+1.…(4分)
(2)由(1)知,cn=an•bn=(3n+1)$•(\frac{1}{2})^{n+1}$.…(5分)
Sn=4×$(\frac{1}{2})^{2}$+7×$(\frac{1}{2})^{3}$+10×$(\frac{1}{2})^{4}$+…+(3n-2)×$(\frac{1}{2})^{n}$+(3n+1)×$(\frac{1}{2})^{n+1}$,①
则$\frac{1}{2}{S}_{n}$=4×$(\frac{1}{2})^{3}$+7×$(\frac{1}{2})^{4}$+10×$(\frac{1}{2})^{5}$+…+(3n-2)×$(\frac{1}{2})^{n+1}$+(3n+1)×$(\frac{1}{2})^{n+2}$,②…(7分)
①-②两式相减得$\frac{1}{2}$Sn=4×$(\frac{1}{2})^{2}$+3×$[(\frac{1}{2})^{3}+(\frac{1}{2})^{4}$+…+$(\frac{1}{2})^{n+1}]$-(3n+1)×$(\frac{1}{2})^{n+2}$=$\frac{1}{4}$+3×$\frac{\frac{1}{4}[1-(\frac{1}{2})^{n}]}{1-\frac{1}{2}}$-(3n+1)×$(\frac{1}{2})^{n+2}$.
所以Sn=$\frac{7}{2}$-(3n+7)×$(\frac{1}{2})^{n+1}$.…(10分)
(3)cn=(3n+1)$•(\frac{1}{2})^{n+1}$,
∴cn+1-cn=(3n+4)$•(\frac{1}{2})^{n+2}$-(3n+1)$•(\frac{1}{2})^{n+1}$=$(1-\frac{3}{2}n)$$•(\frac{1}{2})^{n+1}$<0,
则数列{cn}单调递减,
∴当n=1时,cn取最大值是1,…(13分)
又∵cn≤$\frac{1}{4}{m^2}$+m+1对一切正整数n恒成立,
∴m2+4m?0,
解得:m?0或m?-4.…(16分)
点评 本题考查了等比数列的通项公式与求和公式、错位相减法、不等式的解法、数列递推关系,考查了推理能力与计算能力,属于难题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | $(0,\frac{3}{2}]$ | C. | $(1,\frac{3}{2}]$ | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | xy=-1 | B. | xy=1 | C. | y2-x2=2 | D. | y2-x2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
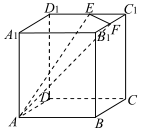 如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )
如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )| A. | $18+3\sqrt{2}$ | B. | $6\sqrt{13}+3\sqrt{2}$ | C. | $6\sqrt{5}+9\sqrt{2}$ | D. | $10+3\sqrt{2}+4\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\sqrt{5}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
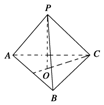 已知点P是正三角形ABC所在平面外一点,PA=PB=PC=$\frac{2}{3}$,AB=1,则PC和平面ABC所成的角是( )
已知点P是正三角形ABC所在平面外一点,PA=PB=PC=$\frac{2}{3}$,AB=1,则PC和平面ABC所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com