
分析 由曲线C的方程可得x2+y2≥1,|x|≤1,|y|≤1,从而可得出曲线C的大体范围,结合图形推导结论.
解答 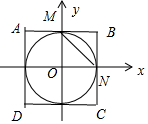 解:设P(x,y)是曲线上一点,则P关于x轴的对称点(x,-y)显然也在曲线C上,
解:设P(x,y)是曲线上一点,则P关于x轴的对称点(x,-y)显然也在曲线C上,
∴曲线C关于x轴对称,
同理可得曲线C关于y轴对称,关于原点对称,故①正确;
∵x2=1-y4=(1-y2)•(1+y2)≥(1-y2),∴x2+y2≥1,即$\sqrt{{x}^{2}+{y}^{2}}$≥1.
∴曲线上任意一点到原点的距离最小值为1,(当且仅当y=0时,x等于1)
故②错误;
由②可得,曲线C所上的点在单位圆x2+y2=1的外部或圆上,∴S>π,
由x2+y4=1可得|x|≤1,|y|≤1,(不能同时取1)
∴曲线C上的点在以2为边长的正方形ABCD内部或边上,∴S<4,
故④正确;
设曲线C的上顶点为M,右顶点为N,则MN=$\sqrt{2}$,
由两点之间线段最短可知曲线C在第一象限内的长度大于$\sqrt{2}$,
同理曲线C在每一象限内的长都大于$\sqrt{2}$,故l>4$\sqrt{2}$,故③正确.
故答案为:3.
点评 本题考查曲线的性质,命题的真假判断,注意运用不等式的性质和数形结合的思想方法,考查推理能力和判断能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$-$\frac{\sqrt{3}}{2}$i | B. | $\frac{3}{4}$-$\frac{\sqrt{3}}{4}$i | C. | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$i | D. | $\frac{3}{4}$+$\frac{\sqrt{3}}{4}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
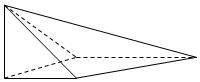 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com