
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 设$\overrightarrow a$与$\overrightarrow b$的夹角为θ,θ∈[0,π],依题意,由($\overrightarrow a$+$\overrightarrow b$)•$\overrightarrow a$=0,可求得cosθ=-$\frac{1}{2}$,从而可得答案.
解答 解:设$\overrightarrow a$与$\overrightarrow b$的夹角为θ,θ∈[0,π].
∵$\overrightarrow a=(1,\sqrt{3})$,$|{\overrightarrow b}|=4$,且($\overrightarrow a$+$\overrightarrow b$)⊥$\overrightarrow a$,
∴$\overrightarrow{a}$•$\overrightarrow{a}$+$\overrightarrow{a}$•$\overrightarrow{b}$=0,即${\overrightarrow{a}}^{2}$+|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ=0,即4+2×4cosθ=0,
∴cosθ=-$\frac{1}{2}$,θ∈[0,π],
∴θ=$\frac{2π}{3}$,
故选:A.
点评 本题考查平面向量的数量积的运算,由($\overrightarrow a$+$\overrightarrow b$)•$\overrightarrow a$=0,求得cosθ=-$\frac{1}{2}$是关键,考查理解与运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{13}$ | B. | $\frac{9}{13}$ | C. | $\frac{10}{13}$ | D. | $\frac{11}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4\sqrt{3}}{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
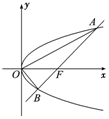 如图,过抛物线y2=2px(p>0)的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.
如图,过抛物线y2=2px(p>0)的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | $(0,\frac{3}{2}]$ | C. | $(1,\frac{3}{2}]$ | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com