
分析 (1)对x的范围进行讨论,去绝对值符号解出;
(2)使用作差法证明.
解答 (1)解:①若x≤-$\frac{1}{2}$,则不等式为-2x-1-(4-x)>2,解得x<-7,
②若-$\frac{1}{2}$<x≤4,则不等式为2x+1-(4-x)>2,解得$\frac{5}{3}$<x≤4,
③若x>4,则不等式为2x+1-(x-4)>2,解得x>4,
综上,原不等式的解集为 {x|x<-7或x>$\frac{5}{3}$}.
(2)证明:∵a>0,b>0
∴$\frac{a}{{\sqrt{b}}}+\frac{b}{{\sqrt{a}}}-\sqrt{a}-\sqrt{b}$=$\frac{{a\sqrt{a}+b\sqrt{b}-a\sqrt{b}-b\sqrt{a}}}{{\sqrt{ab}}}$=$\frac{{(a-b)\sqrt{a}+(b-a)\sqrt{b}}}{{\sqrt{ab}}}$=$\frac{{{{(\sqrt{a}-\sqrt{b})}^2}(\sqrt{a}+\sqrt{b})}}{{\sqrt{ab}}}≥0$.
∴$\frac{a}{{\sqrt{b}}}+\frac{b}{{\sqrt{a}}}≥\sqrt{a}+\sqrt{b}$.
点评 本题考查了含绝对值不等式的解法,不等式的证明,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{15}}}{6}$ | B. | $\frac{{\sqrt{15}}}{4}$ | C. | $\frac{{\sqrt{15}}}{2}$ | D. | $\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
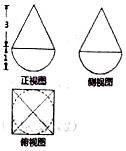 一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{\sqrt{2}π}}{6}$ | C. | $2+\frac{2π}{3}$ | D. | $2+\frac{{\sqrt{2}π}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
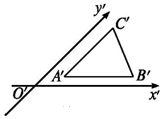
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
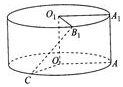 将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,∠AOC=120°,∠A1O1B1=60°,其中B1与C在平面AA1O1O的同侧,则异面直线B1C与AA1所成角的大小是45°.
将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,∠AOC=120°,∠A1O1B1=60°,其中B1与C在平面AA1O1O的同侧,则异面直线B1C与AA1所成角的大小是45°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com