
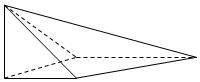
 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.分析 (1)由AD∥BC,知异面直线BC与SD所成角是∠SDA或其补角,由此能求出异面直线BC与SD所成角的大小.
(2)推导出SA⊥BC,AB⊥BC,从而BC⊥面SAB,进而SB是SC在平面SAB上的射影,∠CSB是SC与底面SAB所成角,由此能求出SC与底面SAB所成角的正切值.
(3)三棱锥D-SBC的体积:VD-SBC=VA-SBC=VS-ABC,由此能求出结果.
解答 解:(1)∵AD∥BC,∴异面直线BC与SD所成角是∠SDA或其补角,
∵SA⊥平面ABCD,AD?平面ABCD,
∴SA⊥AD,在Rt△SAD中,∵SA=AD,∴∠SDA=45°,
∴异面直线BC与SD所成角的大小为45o.
(2)∵SA⊥面ABCD,BC?面ABCD,∴SA⊥BC,
又∵AB⊥BC,SA∩AB=A,
∴BC⊥面SAB,
∴SB是SC在平面SAB上的射影,
∴∠CSB是SC与底面SAB所成角
在Rt△CSB中tan∠CSB=$\frac{BC}{SC}=\frac{2}{{\sqrt{2}}}=\sqrt{2}$,
∴SC与底面SAB所成角的正切值为$\sqrt{2}$.
(3)∵AD∥BC,∴D到平面SBC的距离与A到平面SBC的距离相等,
∵SA⊥平面ABC,
∴三棱锥D-SBC的体积:
VD-SBC=VA-SBC=VS-ABC
=$\frac{1}{3}×{S}_{△ABC}×SA$=$\frac{1}{3}×(\frac{1}{2}×1×2)×1$=$\frac{1}{3}$.
点评 本题考查异面直线所成角的求法,考查线面角的正弦值的求法,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系的合理运用,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,考查创新意识、应用意识,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | {3,5,7} | B. | {3,7} | C. | {4,5,6} | D. | {5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
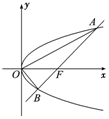 如图,过抛物线y2=2px(p>0)的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.
如图,过抛物线y2=2px(p>0)的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -21007excosx | B. | -21007ex(cosx-sinx) | ||
| C. | 21008exsinx | D. | 21008ex(sinx+cosx) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com