
分析 根据题意,由一元二次方程的性质,可得x2+ax+b2=0有实根的充要条件为a2+b2≥4;
(1)由题意分析可得,这是古典概型,由a、b分别从{-1,0,1},{-3,-2,-1,0,1}中任取的数字,易得一共可以得到15个不同方程,得满足a2+b2≥4的全部情况数目,结合古典概型公式,计算可得答案;
(2)由题意分析可得,这是几何概型,将a,b表示为平面区域,进而可得其中满足a2+b2≥4的区域的面积,由几何概型公式,计算可得答案
解答 解:根据题意,方程x2+2ax-b2+4=0,有实根则△≥0即a2+b2≥4;
(1)由题意,a,b是分别从{-1,0,1},{-3,-2,-1,0,1}中任取的数字;
则a有3种取法,b有5种取法,共有5不同的情况,可以得到15个不同方程,
满足a2+b2≥4的有(-1,-3)(0,-3)(1,-3)(-1,-2)(0,-2)(1,-2)共有6种情况满足方程有实根,
∴p=$\frac{6}{15}=\frac{2}{5}$;
(2)a是从区间[-2,2]中任取的一个数字,b从是区间[-2,2]中任取的一个数字,
由题意得:a,b满足的区域为边长是4 的正方形,面积为16,
使得方程有实根的,a,b满足a2+b2≥4,区域面积为4π,由几何概型的公式得到方程有实根的概率为$\frac{16-4π}{16}=1-\frac{π}{4}$.
点评 本题考查几何概型和古典概型,放在一起的目的是把两种概型加以比较,注意两者的不同


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
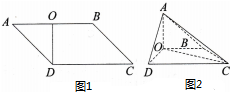 如图1,在∠A=45°的平行四边形ABCD中,DO垂直平分AB,且AB=2,现将△ADO沿DO折起(如图2),使AC=$\sqrt{6}$.
如图1,在∠A=45°的平行四边形ABCD中,DO垂直平分AB,且AB=2,现将△ADO沿DO折起(如图2),使AC=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (7,2) | B. | (7,-14) | C. | (7,-4) | D. | (7,-8) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com