
分析 求出平面ABCD的法向量,然后利用点到平面的距离公式求解即可.
解答 解:四棱锥P-ABCD中,$\overrightarrow{AB}$=(4,-2,3),$\overrightarrow{AD}$=(-4,1,0),$\overrightarrow{AP}$(-6,2,-8),
设平面ABCD的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=0}\\{\overrightarrow{n}•\overrightarrow{AD}=0}\end{array}\right.$,
可得$\left\{\begin{array}{l}{4x-2y+3z=0}\\{-4x+y=0}\end{array}\right.$,
不妨令x=3,则y=12,z=4,
可得$\overrightarrow{n}$=(3,12,4);
则$\overrightarrow{AP}$=(-6,2,-8)在平面ABCD上的射影就是这个四棱锥的高h,
所以h=|$\overrightarrow{AP}$||cos<$\overrightarrow{AP}$,$\overrightarrow{n}$>|=|$\frac{\overrightarrow{AP}•\overrightarrow{n}}{|\overrightarrow{n}|}$|=$\frac{|-18+24-32|}{13}$=2;
所以该四棱锥的高为2.
故答案为:2.
点评 本题考查空间点到平面的距离公式的应用,向量的数量积的应用,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
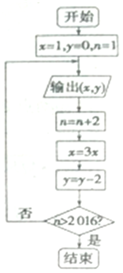 已知某算法的程序框图如图所示,若将输出(x,y)的值依次记(x1,y1),(x2,y2),…(xn,yn),…
已知某算法的程序框图如图所示,若将输出(x,y)的值依次记(x1,y1),(x2,y2),…(xn,yn),…查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com