
分析 (Ⅰ)利用x=ρcosθ,y=ρsinθ,x2+y2=ρ2,求曲线C1,C2的极坐标方程;
(Ⅱ)$\frac{{|{OB}|}}{{|{OA}|}}=\frac{ρ_2}{ρ_1}$=$\frac{1}{4}×2sinα({\sqrt{3}cosα+sinα})$=$\frac{1}{4}({\sqrt{3}sin2α-cos2α+1})$=$\frac{1}{4}[{2sin({2α-\frac{π}{6}})+1}]$,即可得出结论.
解答 解:(Ⅰ)因为x=ρcosθ,y=ρsinθ,x2+y2=ρ2,C1的极坐标方程为$\sqrt{3}ρcosθ+ρsinθ-4=0$,
C2的普通方程为x2+(y-1)2=1,即x2+y2-2y=0,对应极坐标方程为ρ=2sinθ.
(Ⅱ)曲线C3的极坐标方程为θ=α(ρ>0,$0<α<\frac{π}{2}$)
设A(ρ1,α),B(ρ2,α),则${ρ_1}=\frac{4}{{\sqrt{3}cosα+sinα}}$,ρ2=2sinα,
所以$\frac{{|{OB}|}}{{|{OA}|}}=\frac{ρ_2}{ρ_1}$=$\frac{1}{4}×2sinα({\sqrt{3}cosα+sinα})$=$\frac{1}{4}({\sqrt{3}sin2α-cos2α+1})$=$\frac{1}{4}[{2sin({2α-\frac{π}{6}})+1}]$,
又$0<α<\frac{π}{2}$,$-\frac{π}{6}<2α-\frac{π}{6}<\frac{5π}{6}$,
所以当$2α-\frac{π}{6}=\frac{π}{2}$,即$α=\frac{π}{3}$时,$\frac{{|{OB}|}}{{|{OA}|}}$取得最大值$\frac{3}{4}$.
点评 本题考查三种方程的转化,考查极坐标方程的运用,考查学生的计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | b>c>a | C. | a>b>c | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
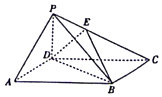 如图所示,在四棱锥P-ABCD中,底要ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.
如图所示,在四棱锥P-ABCD中,底要ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com