
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
分析 设直线l的方程为y=k1(x+2),代入x2+2y2=2,得(1+2k12)x2+8k12x+8k12-2=0,然后由根与系数的关系求解能够得到k1k2的值.
解答 解:设P1(x1,y1),P2(x2,y2),中点P(x0,y0),
设直线l的方程为y=k1(x+2),代入x2+2y2=2,得(1+2k12)x2+8k12x+8k12-2=0,
所以x1+x2=-$\frac{8{{k}_{1}}^{2}}{1+2{{k}_{1}}^{2}}$.而y1+y2=k1(x1+x2+4)=$\frac{4{k}_{1}}{1+2{{k}_{1}}^{2}}$.
所以OP的斜率k2=$\frac{{y}_{0}}{{x}_{0}}=\frac{{y}_{1}+{y}_{2}}{{x}_{1}+{x}_{2}}$=-$\frac{1}{2{k}_{1}}$
所以k1k2=-$\frac{1}{2}$
故选:D
点评 本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答.属于中档题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
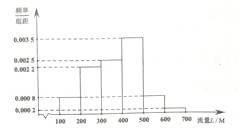 某学校为鼓励家校互动,与某手机通讯商合作,为教师伴侣流量套餐,为了解该校教师手机流量使用情况,通过抽样,得到100位教师近2年每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如下:若将每位教师的手机月平均使用流量分布视为其手机月使用流量,并将频率为概率,回答以下问题.
某学校为鼓励家校互动,与某手机通讯商合作,为教师伴侣流量套餐,为了解该校教师手机流量使用情况,通过抽样,得到100位教师近2年每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如下:若将每位教师的手机月平均使用流量分布视为其手机月使用流量,并将频率为概率,回答以下问题.| 套餐名称 | 月套餐费(单位:元) | 月套餐流量(单位:M) |
| A | 20 | 300 |
| B | 30 | 500 |
| C | 38 | 700 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ef(1)<f(2) | B. | e3f(-1)>f(2) | C. | e2f(-1)<f(1) | D. | ef(-2)<f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8068 | B. | 2017 | C. | -8027 | D. | -2013 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)<f(4) | B. | f(0)=f(4) | C. | f(0)>f(4) | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com