
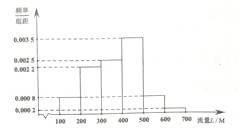
 某学校为鼓励家校互动,与某手机通讯商合作,为教师伴侣流量套餐,为了解该校教师手机流量使用情况,通过抽样,得到100位教师近2年每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如下:若将每位教师的手机月平均使用流量分布视为其手机月使用流量,并将频率为概率,回答以下问题.
某学校为鼓励家校互动,与某手机通讯商合作,为教师伴侣流量套餐,为了解该校教师手机流量使用情况,通过抽样,得到100位教师近2年每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如下:若将每位教师的手机月平均使用流量分布视为其手机月使用流量,并将频率为概率,回答以下问题.| 套餐名称 | 月套餐费(单位:元) | 月套餐流量(单位:M) |
| A | 20 | 300 |
| B | 30 | 500 |
| C | 38 | 700 |
分析 (1)记“从该校随机抽取一名教师,该教师手机月使用流量不超过300M”为事件D,依题意,P(D)=0.3,从该校教师中随机抽取3人,设这3人中手机月使用流量不超过300M的人数为X,则X~B(3,0.3),由此能求出从该校教师中随机抽取3人,至多有一人手机月使用流量不300M的概率.
(2)依题意,从该校随机抽取一名教师,该教师手机月使用流量L∈(300,500]的概率为0.6,L∈(500,700]的概率为0.1,分别求出三各套餐的数学期望,能得到学校订购B套餐最经济.
解答 解:(1)记“从该校随机抽取一名教师,该教师手机月使用流量不超过300M”为事件D,
依题意,P(D)=(0.0008+0.0022)×100=0.3,
从该校教师中随机抽取3人,设这3人中手机月使用流量不超过300M的人数为X,则X~B(3,0.3),
∴从该校教师中随机抽取3人,至多有一人手机月使用流量不300M的概率为:
P(X=0)+P(X=1)=${C}_{3}^{0}(0.3)^{0}(0.7)^{3}+{C}_{3}^{1}(0.3)(0.7)^{2}$=0.784.
(2)依题意,从该校随机抽取一名教师,
该教师手机月使用流量L∈(300,500]的概率为:(0.0025+0.0035)×100=0.6,
L∈(500,700]的概率为:(0.0008+0.0002)×100=0.1,
当学校订购A套餐时,设学校为一位教师承担的月费用为X元,
则X的所有可能取值为20,35,50,且P(X=20)=0.3,P(X=35)=0.6,P(X=50)=0.1,
∴X的分布列为:
| X | 20 | 35 | 50 |
| P | 0.3 | 0.6 | 0.1 |
| Y | 30 | 45 |
| P | 0.9 | 0.1 |
点评 本题考查频率分布直方图、独立重复试验、数学期望等基础知识,考查抽象概括能力、数据处理能力、运算求解能力,考查应用意识、创新意识,考查统计与概率思想、分类与整合思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | b>c>a | C. | a>b>c | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$-1 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{{e}^{2}}{4}$,$\frac{{e}^{2}}{4}$] | B. | [-$\frac{{e}^{2}}{2}$,$\frac{{e}^{2}}{2}$] | C. | [-$\frac{{e}^{2}}{3}$,$\frac{{e}^{2}}{3}$] | D. | [-e2,e2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com