练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．sin300°+cos390°+tan（-135°）=（　　）
    A．$\sqrt{3}$-1B．1C．$\sqrt{3}$D．$\sqrt{3}$+1

    分析 由条件利用诱导公式化简所给的三角函数式，可得结果．

    解答 解：sin300°+cos390°+tan（-135°）=sin（-60°）+cos30°+tan（180°-135°）
    =-sin60°+cos30°+tan45°=-$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$+1=1，
    故选：B．

    点评 本题主要考查利用诱导公式进行化简求值，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    15．已知单位向量$\overrightarrow a$，$\overrightarrow b$满足$\overrightarrow a•（2\overrightarrow a-3\overrightarrow b）=\frac{1}{2}$，则向量$\overrightarrow a$与$\overrightarrow b$的夹角为60°（或$\frac{π}{3}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

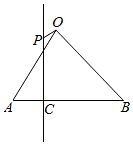    16．如图，在等腰直角△ABO中，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，C为AB上靠近A点的三等分点，过C作AB的垂线l，设P为垂线上任一点，$\overrightarrow{OP}$=$\overrightarrow{p}$，则$\overrightarrow{p}$•（$\overrightarrow{b}$-$\overrightarrow{a}$）=（　　）
    A．$\frac{1}{3}$B．-$\frac{1}{3}$C．-$\frac{3}{2}$D．$\frac{3}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

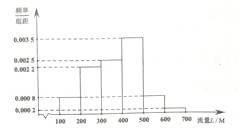    13．某学校为鼓励家校互动，与某手机通讯商合作，为教师伴侣流量套餐，为了解该校教师手机流量使用情况，通过抽样，得到100位教师近2年每人手机月平均使用流量L（单位：M）的数据，其频率分布直方图如下：若将每位教师的手机月平均使用流量分布视为其手机月使用流量，并将频率为概率，回答以下问题．
    （1）从该校教师中随机抽取3人，求这3人中至多有1人月使用流量不超过300M的概率；
    （2）现该通讯商推出三款流量套餐，详情如下：
     套餐名称月套餐费（单位：元） 月套餐流量（单位：M）
     A 20 300
     B 30 500
     C 38 700
    这三款套餐都有如下附加条款：套餐费月初一次性收取，手机使用一旦超出套餐流量，系统就自动帮用户充值200M流量，资费20元；如果又超出充值流量，系统就再次自动帮用户充值200M流量，资费20元/次，依此类推，如果当流量有剩余，系统将自动清零，无法转入次月使用．
    学校欲订购其中一款流量套餐，为教师支付月套餐费，并承担系统自动充值的流量资费的75%，其余部分由教师个人承担，问学校订购哪一款套餐最经济？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．复数1-2i的共轭复数是1+2i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知函数y=$\frac{f（x）}{{e}^{x}}$是偶函数且在[0，+∞）上单调递增，则下列说法中正确的是（　　）
    A．ef（1）＜f（2）B．e3f（-1）＞f（2）C．e2f（-1）＜f（1）D．ef（-2）＜f（-1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．化简计算：
    （1）已知tanθ=2，求值：$\frac{sin（θ+\frac{π}{2}）cos（\frac{π}{2}-θ）{-cos}^{2}（π-θ）}{1{+sin}^{2}θ}$；
    （2）ln（$\sqrt{{x}^{2}+1}$+x）+ln（$\sqrt{{x}^{2}+1}$-x）+lg22+（1+lg2）•lg5-2sin30°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知数列{an}的前n项和为Sn，满足Sn=$\frac{t}{t-1}$an-n（t＞0且t≠1，n∈N*）
    （1）证明：数列{an+1}为等比数列，并求数列{an}的通项公式（用t，n表示）
    （2）当t=2时，令cn=$\frac{{a}_{n}+1}{{a}_{n}•{a}_{n+1}}$，证明$\frac{2}{3}$≤c1+c2+c3+…+cn＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知Sn为等比数列{an}的前n项和•且S4=S3+3a3，a2=9．
    （1）求数列{an}的通项公式
    （2）设bn=（2n-1）an，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    同步练习册答案