
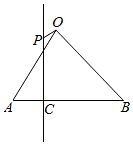
 如图,在等腰直角△ABO中,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点,$\overrightarrow{OP}$=$\overrightarrow{p}$,则$\overrightarrow{p}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=( )
如图,在等腰直角△ABO中,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点,$\overrightarrow{OP}$=$\overrightarrow{p}$,则$\overrightarrow{p}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=( )| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
分析 P在线段AB的垂直平分线上,通过向量的加减运算,向量的数量积的运算即可得到结果.
解答 解:∵等腰直角△ABO中,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,
C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点,$\overrightarrow{OP}$=$\overrightarrow{p}$,
设AB中点为D,则$\overrightarrow{OP}$=$\overrightarrow{OC}$+$\overrightarrow{CP}$,$\overrightarrow{OC}$=$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{2}{3}$$\overrightarrow{OA}$.
∵$\overrightarrow{CP}$⊥$\overrightarrow{AB}$,∴$\overrightarrow{CP}$•$\overrightarrow{BA}$=$\overrightarrow{CP}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=0,
∴$\overrightarrow{p}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=$\overrightarrow{OP}$•($\overrightarrow{OB}$-$\overrightarrow{OA}$)=($\overrightarrow{OC}$+$\overrightarrow{CP}$)•$\overrightarrow{AB}$=$\overrightarrow{OC}•\overrightarrow{AB}$+$\overrightarrow{CP}•\overrightarrow{AB}$
=$\overrightarrow{OC}$•$\overrightarrow{AB}$+0=($\frac{1}{3}$$\overrightarrow{OB}$+$\frac{2}{3}$$\overrightarrow{OA}$)•($\overrightarrow{OB}$-$\overrightarrow{OA}$)=$\frac{{\overrightarrow{OB}}^{2}}{3}$-$\frac{{2\overrightarrow{OA}}^{2}}{3}$+$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{3}$
=$\frac{1}{3}$-$\frac{2}{3}$+0=-$\frac{1}{3}$,
故选:B.
点评 本题考查线段垂直平方线的性质、向量的运算法则、向量模的平方等于向量的平方,考查转化计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
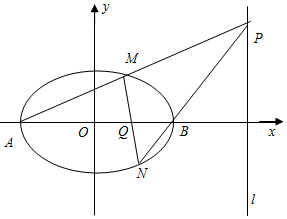 在平面直角坐标系xOy中,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左右顶点,离心率为$\frac{1}{2}$,且椭圆过定点$(1,\frac{3}{2})$,P为椭圆右准线上任意一点,直线PA,PB分别交椭圆于M,N.
在平面直角坐标系xOy中,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左右顶点,离心率为$\frac{1}{2}$,且椭圆过定点$(1,\frac{3}{2})$,P为椭圆右准线上任意一点,直线PA,PB分别交椭圆于M,N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$-1 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com