
分析 根据数列的递推公式可得数列{$\frac{1}{{a}_{n}}$+1}是等比数列,首项为$\frac{1}{{a}_{1}}$+1=2,公比为2,再代值得到bn+1=(n-λ)•2n,根据数列的单调性即可求出λ的范围.
解答 解:∵${a_1}=1,\frac{1}{{{a_{n+1}}}}=\frac{2}{a_n}+1,({n∈{N^*}})$,
∴$\frac{1}{{a}_{n+1}}$=$\frac{2}{{a}_{n}}$+1,化为$\frac{1}{{a}_{n+1}}$+1=$\frac{2}{{a}_{n}}$+2
∴数列{$\frac{1}{{a}_{n}}$+1}是等比数列,首项为$\frac{1}{{a}_{1}}$+1=2,公比为2,
∴$\frac{1}{{a}_{n}}$+1=2n,
∴bn+1=(n-λ)($\frac{1}{{a}_{n}}$+1)=(n-λ)•2n,
∵b1=-λ,且数列{bn}是单调递增数列,
∴b2>b1,
∴(1-λ)•2>-λ,
解得λ<2,
故答案为:λ<2
点评 本题考查了变形利用等比数列的通项公式的方法、单调递增数列,考查了推理能力与计算能力,属于中档题.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:选择题
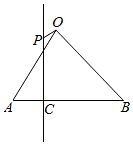 如图,在等腰直角△ABO中,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点,$\overrightarrow{OP}$=$\overrightarrow{p}$,则$\overrightarrow{p}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=( )
如图,在等腰直角△ABO中,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点,$\overrightarrow{OP}$=$\overrightarrow{p}$,则$\overrightarrow{p}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=( )| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 第4天 | 第32天 | 第60天 | 第90天 |
| 价格(千元) | 23 | 30 | 22 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)<f(4) | B. | f(0)=f(4) | C. | f(0)>f(4) | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com