
���� ��1��������{an}�Ĺ���Ϊd������{bn}�Ĺ���Ϊq����a1b1+a2b2+a3b3+��+anbn=��n-1��•2n+2+4�зֱ���n=1��2��3���õ�����d��q�ķ����飬��ⷽ����ɵ�$\left\{\begin{array}{l}{{d}_{1}=-\frac{2}{3}}\\{{q}_{1}=6}\end{array}\right.$��$\left\{\begin{array}{l}{{d}_{2}=2}\\{{q}_{2}=2}\end{array}\right.$������d=q=2�������⣬�Ӷ����an=2n��${b}_{n}={2}^{n}$��
��2����an=2n����sin$\frac{{a}_{n}��}{4}=sin\frac{n��}{2}$����${b}_{n}=\frac{1}{��1-\frac{1}{{a}_{1}}����1-\frac{1}{{a}_{2}}������1-\frac{1}{{a}_{n}}��\sqrt{{a}_{n}+1}}$����ԭ����ʽת��Ϊ$��sin\frac{n��}{2}��{b}_{n}$����$\frac{{b}_{n+1}}{{b}_{n}}=\frac{2��n+1��}{\sqrt{2n+1}•\sqrt{2n+3}}��1$���ɵ�����{bn}�����������������������ʵ���ˣ�ʹ�ò���ʽ$��sin\frac{n��}{2}��{b}_{n}$��һ��n��N*���������֢�n=4m+4��n=4m+2��m��N����n=4m+1��m��N����n=4m+3��m��Nʱ����0�����˵�ֵ��
��3���������֪��d=0ʱ��������d��0ʱ�����${{c}_{39}}^{2}={c}_{1}{c}_{k}$���ã�2014-38d��[2014+��k-39��d]=20142����k=$\frac{39d-53��77}{d-53}$=$\frac{39��d-53��+53��39-53��77}{d-53}$=$39-\frac{53��38}{d-53}=39+\frac{53��38}{53-d}$��N*������d��0��c1��0����˵����п���ȡֵ�ô𰸣�
��� �⣺��1��������{an}�Ĺ���Ϊd������{bn}�Ĺ���Ϊq��
��a1b1+a2b2+a3b3+��+anbn=��n-1��•2n+2+4��
��n=1��2��3���ֱ��a1b1=4��a1b1+a2b2=20��a1b1+a2b2+a3b3=68��
��a1=2��
��$\left\{\begin{array}{l}{{a}_{1}={b}_{1}=2}\\{{a}_{2}{b}_{2}=16}\\{{a}_{3}{b}_{3}=48}\end{array}\right.$����$\left\{\begin{array}{l}{��2+d��•2q=16}\\{��2+2d��•2{q}^{2}=48}\end{array}\right.$�����$\left\{\begin{array}{l}{{d}_{1}=-\frac{2}{3}}\\{{q}_{1}=6}\end{array}\right.$��$\left\{\begin{array}{l}{{d}_{2}=2}\\{{q}_{2}=2}\end{array}\right.$��
������d=q=2�������⣬$d=-\frac{2}{3}��q=6$�������⣬��ȥ��
��an=2n��${b}_{n}={2}^{n}$��
��2����an=2n����sin$\frac{{a}_{n}��}{4}=sin\frac{n��}{2}$��
��${b}_{n}=\frac{1}{��1-\frac{1}{{a}_{1}}����1-\frac{1}{{a}_{2}}������1-\frac{1}{{a}_{n}}��\sqrt{{a}_{n}+1}}$��
��ʽsin$\frac{{a}_{n}��}{4}$��$\frac{1}{�ˣ�1-\frac{1}{{a}_{1}}����1-\frac{1}{{a}_{2}}������1-\frac{1}{{a}_{n}}��\sqrt{{a}_{n}+1}}$�ȼ���$��sin\frac{n��}{2}��{b}_{n}$��
��bn��0����$\frac{{b}_{n+1}}{{b}_{n}}=\frac{2��n+1��}{\sqrt{2n+1}•\sqrt{2n+3}}��1$��
��bn+1��bn������{bn}����������
�������������ʵ���ˣ�ʹ�ò���ʽ$��sin\frac{n��}{2}��{b}_{n}$��һ��n��N*����������
�ٵ�n=4m+4��n=4m+2��m��Nʱ��sin$\frac{n��}{2}=0$������ʽ$��sin\frac{n��}{2}��{b}_{n}$�������
�ڵ�n=4m+1��m��Nʱ��sin$\frac{n��}{2}=1$���ˣ�$��{b}_{n}��_{min}=\frac{2\sqrt{3}}{3}$��
�۵�n=4m+3��m��Nʱ��sin$\frac{n��}{2}=-1$��$-�ˣ���{b}_{n}��_{min}={b}_{3}=\frac{16\sqrt{7}}{35}$��
���ϣ��ˡʣ�$-\frac{16\sqrt{7}}{35}��\frac{2\sqrt{3}}{3}$�����ɦ��Ƿ�0��������֪���ڦ�=1��-1���������⣬�ᣩ����������
��3���������֪��d=0ʱ������
��d��0ʱ��c39=c1+38d=2014����c1=2014-38d��
ck=c39+��k-39��d=2014+��k-39��d��
��${{c}_{39}}^{2}={c}_{1}{c}_{k}$���ã�2014-38d��[2014+��k-39��d]=20142����
k=$\frac{39d-53��77}{d-53}$=$\frac{39��d-53��+53��39-53��77}{d-53}$=$39-\frac{53��38}{d-53}=39+\frac{53��38}{53-d}$��N*��
�֡�$\left\{\begin{array}{l}{{c}_{1}=2014-38d=38��53-d����0}\\{d��0}\end{array}\right.$��0��53-d��53��
��53-d=1��2��19��53��
��d=0��52��51��34��
���d�����п���ȡֵ֮��Ϊ137��
���� ���⿼�����е���ʽ�����������÷�����֤�����в���ʽ�������˷������۵���ѧ˼�뷽������ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {0��1��2} | B�� | {-1��1��2} | C�� | {-1��0��2} | D�� | {-1��0��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
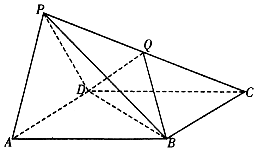 ��ͼ������P-ABCD�ĵ���ABCD��ƽ���ı��Σ�����PAD�DZ߳�Ϊ2���������Σ�AB=BD=$\sqrt{7}$��PB=3��
��ͼ������P-ABCD�ĵ���ABCD��ƽ���ı��Σ�����PAD�DZ߳�Ϊ2���������Σ�AB=BD=$\sqrt{7}$��PB=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
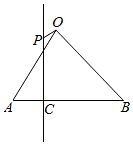 ��ͼ���ڵ���ֱ�ǡ�ABO�У���$\overrightarrow{OA}$=$\overrightarrow{a}$��$\overrightarrow{OB}$=$\overrightarrow{b}$��|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1��CΪAB�Ͽ���A������ȷֵ㣬��C��AB�Ĵ���l����PΪ��������һ�㣬$\overrightarrow{OP}$=$\overrightarrow{p}$����$\overrightarrow{p}$•��$\overrightarrow{b}$-$\overrightarrow{a}$��=��������
��ͼ���ڵ���ֱ�ǡ�ABO�У���$\overrightarrow{OA}$=$\overrightarrow{a}$��$\overrightarrow{OB}$=$\overrightarrow{b}$��|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1��CΪAB�Ͽ���A������ȷֵ㣬��C��AB�Ĵ���l����PΪ��������һ�㣬$\overrightarrow{OP}$=$\overrightarrow{p}$����$\overrightarrow{p}$•��$\overrightarrow{b}$-$\overrightarrow{a}$��=��������| A�� | $\frac{1}{3}$ | B�� | -$\frac{1}{3}$ | C�� | -$\frac{3}{2}$ | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
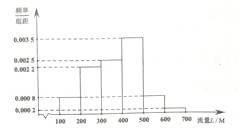 ijѧУΪ������У��������ij�ֻ�ͨѶ�̺�����Ϊ��ʦ���������ײͣ�Ϊ�˽��У��ʦ�ֻ�����ʹ�������ͨ���������õ�100λ��ʦ��2��ÿ���ֻ���ƽ��ʹ������L����λ��M�������ݣ���Ƶ�ʷֲ�ֱ��ͼ���£�����ÿλ��ʦ���ֻ���ƽ��ʹ�������ֲ���Ϊ���ֻ���ʹ������������Ƶ��Ϊ���ʣ��ش��������⣮
ijѧУΪ������У��������ij�ֻ�ͨѶ�̺�����Ϊ��ʦ���������ײͣ�Ϊ�˽��У��ʦ�ֻ�����ʹ�������ͨ���������õ�100λ��ʦ��2��ÿ���ֻ���ƽ��ʹ������L����λ��M�������ݣ���Ƶ�ʷֲ�ֱ��ͼ���£�����ÿλ��ʦ���ֻ���ƽ��ʹ�������ֲ���Ϊ���ֻ���ʹ������������Ƶ��Ϊ���ʣ��ش��������⣮| �ײ����� | ���ײͷѣ���λ��Ԫ�� | ���ײ���������λ��M�� |
| A | 20 | 300 |
| B | 30 | 500 |
| C | 38 | 700 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ef��1����f��2�� | B�� | e3f��-1����f��2�� | C�� | e2f��-1����f��1�� | D�� | ef��-2����f��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��0����f��4�� | B�� | f��0��=f��4�� | C�� | f��0����f��4�� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com