
分析 利用向量的数量积与夹角关系,转化求解即可.
解答 解:由题单位向量$\overrightarrow a$,$\overrightarrow b$满足$\overrightarrow a•(2\overrightarrow a-3\overrightarrow b)=\frac{1}{2}$,2-3$\overrightarrow{a}•\overrightarrow{b}$=$\frac{1}{2}$.
可得$\overrightarrow a•\overrightarrow b=\frac{1}{2},cos<\overrightarrow a,\overrightarrow b>=\frac{\overrightarrow a•\overrightarrow b}{{|{\overrightarrow a}||{\overrightarrow b}|}}=\frac{1}{2}$,
故向量$\overrightarrow a$与$\overrightarrow b$的夹角为60°(或写成$\frac{π}{3}$).
故答案为:60°(或$\frac{π}{3}$).
点评 本题考查向量的数量积与夹角的求法,考查计算能力.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
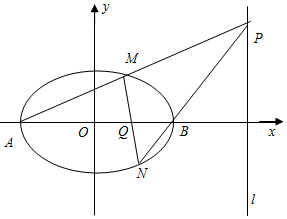 在平面直角坐标系xOy中,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左右顶点,离心率为$\frac{1}{2}$,且椭圆过定点$(1,\frac{3}{2})$,P为椭圆右准线上任意一点,直线PA,PB分别交椭圆于M,N.
在平面直角坐标系xOy中,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左右顶点,离心率为$\frac{1}{2}$,且椭圆过定点$(1,\frac{3}{2})$,P为椭圆右准线上任意一点,直线PA,PB分别交椭圆于M,N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | b>c>a | C. | a>b>c | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
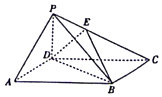 如图所示,在四棱锥P-ABCD中,底要ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.
如图所示,在四棱锥P-ABCD中,底要ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$-1 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{3}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com