
| A. | [-$\frac{{e}^{2}}{4}$,$\frac{{e}^{2}}{4}$] | B. | [-$\frac{{e}^{2}}{2}$,$\frac{{e}^{2}}{2}$] | C. | [-$\frac{{e}^{2}}{3}$,$\frac{{e}^{2}}{3}$] | D. | [-e2,e2] |
分析 由题意可知函数y=丨f(x)丨单调递增,分类讨论,根据函数的性质及对勾函数的性质,即可求得实数a的取值范围.
解答 解:由任意的x1,x2∈[1,2],且x1<x2,由[|f(x1)|-|f(x2)|](x1-x2)>0,
则函数y=丨f(x)丨单调递增,
当a≥0,f(x)在[1,2]上是增函数,则f(1)≥0,解得:0≤a≤$\frac{{e}^{2}}{2}$,
当a<0时,丨f(x)丨=f(x),令$\frac{{e}^{x}}{2}$=-$\frac{a}{{e}^{x}}$,
解得:x=ln$\sqrt{-2a}$,
由对勾函数的单调递增区间为[ln$\sqrt{-2a}$,+∞),
故ln$\sqrt{-2a}$≤1,解得:-$\frac{{e}^{2}}{2}$≤a<0,
综上可知:a的取值范围为[-$\frac{{e}^{2}}{2}$,$\frac{{e}^{2}}{2}$],
故选B.
点评 本题考查函数的综合应用,考查对数函数的运算,对勾函数的性质,考查分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:解答题
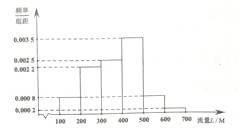 某学校为鼓励家校互动,与某手机通讯商合作,为教师伴侣流量套餐,为了解该校教师手机流量使用情况,通过抽样,得到100位教师近2年每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如下:若将每位教师的手机月平均使用流量分布视为其手机月使用流量,并将频率为概率,回答以下问题.
某学校为鼓励家校互动,与某手机通讯商合作,为教师伴侣流量套餐,为了解该校教师手机流量使用情况,通过抽样,得到100位教师近2年每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如下:若将每位教师的手机月平均使用流量分布视为其手机月使用流量,并将频率为概率,回答以下问题.| 套餐名称 | 月套餐费(单位:元) | 月套餐流量(单位:M) |
| A | 20 | 300 |
| B | 30 | 500 |
| C | 38 | 700 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)<f(4) | B. | f(0)=f(4) | C. | f(0)>f(4) | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com