
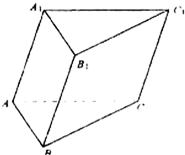
 如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为
如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(b)-f(a) |
| b-a |
| 1 |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 区间 | 122~126 | 126~130 | 130~134 | 134~138 | 138~142 |
| 人数 | 5 | 8 | 10 | 22 | 33 |
| 区间 | 142~146 | 146~150 | 150~154 | 154~158 | |
| 人数 | 20 | 11 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
| 3 |
| 4 |
| π |
| 4 |
| π |
| 2 |
4+
| ||
| 2 |
| π |
| 4 |
| π |
| 2 |
| (5sin2α+11cos2α-8)(tanα+cotα) | ||||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| m+a |
| n |
| n+a |
| h1h2 |
| 3 |
| 5 |
| 3 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com