
| A、[-1+e-1,1+e] |
| B、[1,1+e] |
| C、[e,1+e] |
| D、[1,e] |


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
| 平面 | 空间 |
| 三角形的两边之和大于第三边 | 四面体的任意三个面的面积之和大于第四个面的面积 |
| 三角形的面积等于任意一边的长度与这个边上高的乘积的二分之一 | 四面体的体积等于任意底面的面积与这个底面上的高的乘积的三分之一 |
| 三角形的面积等于其内切圆的半径与三角形周长乘积的二分之一 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(0,1) |
| B、(1,2) |
| C、(0,2) |
| D、[2,+∞] |
查看答案和解析>>
科目:高中数学 来源: 题型:
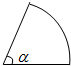 现要用篱笆围成一个面积为S扇形菜园(如图所示),问要使这个菜园所用篱笆最短,则这个扇形的半径和圆心角各为( )
现要用篱笆围成一个面积为S扇形菜园(如图所示),问要使这个菜园所用篱笆最短,则这个扇形的半径和圆心角各为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、4 | B、2 | C、3 | D、5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 函数f(x)=2sin(ωx+φ)(ω>0,
函数f(x)=2sin(ωx+φ)(ω>0,| π |
| 2 |
| A、2 | ||
B、
| ||
C、-
| ||
| D、-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OA |
| OB |
| OP |
| OA |
| OQ |
| OB |
| PQ |
| 1 |
| 5 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 75 |
| k |
| x |
| A、23 | B、24 | C、25 | D、26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com