
椭圆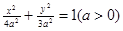 的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是 .
的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是 .
3a2
解析试题分析:设椭圆的右焦点为E.如图: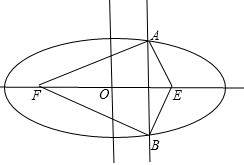
由椭圆的定义得:△FAB的周长:AB+AF+BF=AB+(4a-AE)+(4a-BE)=8a+AB-AE-BE;
∵AE+BE≥AB;
∴AB-AE-BE≤0,当AB过点E时取等号;
∴AB+AF+BF=8a+AB-AE-BE≤8a;
即直线x=m过椭圆的右焦点E时△FAB的周长最大;
此时△FAB的高为:EF=2a.
此时直线x=m=c=1;
把x=1代入椭圆的方程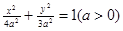 得:y=±
得:y=±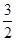 .
.
∴AB=3a.所以:△FAB的面积等于:S△FAB= ×3a×EF=
×3a×EF= ×3a×2a=3a2故答案为3a2
×3a×2a=3a2故答案为3a2
考点:本题主要考查椭圆的定义及几何性质,三角形面积计算。
点评:中档题,在解决涉及到圆锥曲线上的“焦点三角形”问题时,圆锥曲线的定义往往是解题的突破口.解决本题的关键在于利用定义求出周长的表达式.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com