
【题目】已知数列![]() 的各项均为正数,前
的各项均为正数,前![]() 项和
项和![]() 满足
满足![]() ;数列
;数列![]() 是等比数列,前
是等比数列,前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知等比数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 前
前![]() 项和为
项和为![]() ;
;
(3)若![]() ,且等比数列
,且等比数列![]() 的公比
的公比![]() ,若存在
,若存在![]() ,使得
,使得![]() ,试求
,试求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)2
(3)2
【解析】
(1)![]() 化为
化为![]() ,由
,由![]() 与
与![]() 关系,即可求出通项;
关系,即可求出通项;
(2)由(1)得![]() ,将已知化为
,将已知化为![]() ,即
,即![]() 是关于
是关于![]() 函数,进而转化为求
函数,进而转化为求![]() 的最值,求出
的最值,求出![]() ,即可求解;
,即可求解;
(3)由(1)(2)![]() ,即为
,即为![]() ,求解关于
,求解关于![]() 的不定方程,构造数列
的不定方程,构造数列![]() ,判断单调性,得出
,判断单调性,得出![]() 的可能值,验证,即可求解.
的可能值,验证,即可求解.
(1)数列![]() 前
前![]() 项和
项和![]() 满足
满足![]() ,
,
即![]() ;
;![]() ,
,
![]() ;
;
![]() ,∵数列
,∵数列![]() 的各项均为正数,
的各项均为正数,
∴![]() ,又
,又![]() ,∴
,∴![]() ,
,![]()
(2).∵等比数列![]() 满足
满足![]() ,
,![]() ,
,
∴![]() ,令
,令![]() ,
,
![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
∴![]() ,即
,即![]() ,而
,而![]() ,∴
,∴![]() ,
,
∴![]() 且此时
且此时![]() ,设等比数列
,设等比数列![]() 的公比为
的公比为![]() ,
,
![]() ,
,![]() ,所以数列
,所以数列![]() 前
前![]() 项和为
项和为
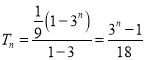 .
.
(3)由![]() ,
,![]() 得:
得:![]() ,
,
正数数列![]() 公比
公比![]() 的等比数列.∵
的等比数列.∵![]() ,
,![]() ,
,
即:![]() ,即:
,即:![]() ,
,
设![]() ,
,![]()
 ,∵
,∵![]() ,
,![]() 时,
时,
上式分子![]() ,
,
数列![]() 单调递增
单调递增
.∴![]() 时,
时,![]() 与
与![]() 矛盾
矛盾
.∴![]() 若
若![]() 时,
时,![]() (∵
(∵![]() )
)
故![]() ,
,![]() 解得
解得![]() 符合条件.
符合条件.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,![]() ,
,![]() //
//![]() ,
,![]() .
.
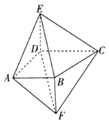
(1)证明:![]() //平面BCE.
//平面BCE.
(2)设平面ABF与平面CDF所成的二面角为θ,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|﹣a.
(1)当a=1时,解不等式f(x)>x+1;
(2)若存在实数x,使得f(x)![]() f(x+1),求实数a的取值范围.
f(x+1),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2019年11月1日到11月20日,某地区甲流疫情新增数据的走势图.
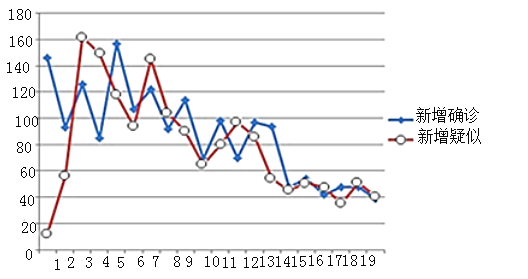
(1)从这20天中任选1天,求新增确诊和新增疑似的人数都超过100的概率;
(2)从新增确诊的人数超过100的日期中任选两天,用X表示新增确诊的人数超过140的天数,求X的分布列和数学期望;
(3)根据这20天统计数据,预测今后该地区甲流疫情的发展趋势.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD的三视图如下图所示,E是侧棱PC上的动点.
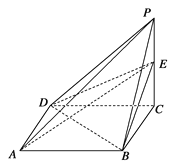
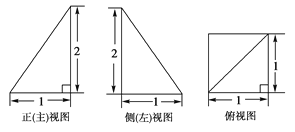
(1)求证:BD⊥AE
(2)若点E为PC的中点,求二面角D-AE-B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() (万元),若年产量不足
(万元),若年产量不足![]() 千件,
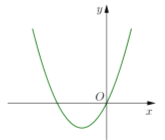
千件, ![]() 的图像是如图的抛物线,此时
的图像是如图的抛物线,此时![]() 的解集为
的解集为![]() ,且
,且![]() 的最小值是
的最小值是![]() ,若年产量不小于
,若年产量不小于![]() 千件,
千件, ![]() ,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
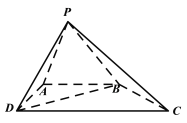
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com